Advertisements
Advertisements
Question
The angle of depression form the top of a tower of a point A on the ground is 30° . On moving a distance of 20 meters from the point A towards the foot of the tower to a point B, the angle of elevation of the top of the tower to from the point B is 60° . Find the height of the tower and its distance from the point A.
Solution
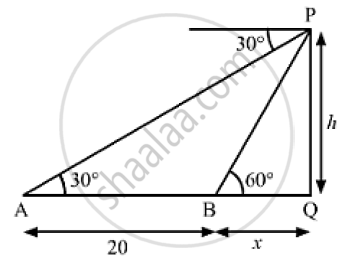
Let PQ be the tower.
We have,
AB = 20m, ∠PAQ = 30° and ∠PBQ = 60°
Let BQ = x and PQ = h
In ΔPBQ,
` tan 60° = (PQ)/(BQ) `
`⇒ sqrt(3) = h/x`
`⇒ = x sqrt(3) ` .......(1)
Also, in ΔAPQ ,
` tan 30° = (PQ)/(AQ)`
`⇒ 1/ sqrt(3) = h/(AB +BQ)`
`⇒ 1/ sqrt(3) = (x sqrt(3))/(20+x)` [Using (1)]
⇒ 20+ x = 3x
⇒ 3x -x = 20
⇒ 2x = 20
`⇒ =20/2`
⇒ x = 10 m
From (i),
`h = 10 sqrt(3)=10xx1.732 =17.32m`
Also, AQ = AB+BQ = 20 + 10 = 30m
So, the height of the tower is 17. 32 m and its distance from the point A is 30 m.
APPEARS IN
RELATED QUESTIONS
The ratio of the height of a tower and the length of its shadow on the ground is `sqrt3 : 1`. What is the angle of elevation of the sun?
The angle of elevation of the top of a hill at the foot of a tower is 60° and the angle of elevation of the top of the tower from the foot of the hill is 30°. If height of the tower is 50 m, find the height of the hill.
A person observed the angle of elevation of the top of a tower as 30°. He walked 50 m towards the foot of the tower along level ground and found the angle of elevation of the top of the tower as 60°. Find the height of the tower.
On a horizontal plane, there is a vertical tower with a flagpole on the top of the tower. At a point 9 meters away from the foot of the tower the angle of elevation of the top and bottom of the flagpole are 60° and 30° respectively. Find the height of the tower and the flagpole mounted on it.
From an aeroplane vertically above a straight horizontal road, the angles of depression of two consecutive milestones on opposite sides of the aeroplane are observed to be α and β. Show that the height in miles of the aeroplane above the road is given by `(tan alpha tan beta)/(tan alpha + tan beta)`
A tower stands vertically on the ground. From a point on the ground which is 20 m away from the foot of the tower, the angle of elevation of its top is found to be 60°. Find the height of the tower. [Take `sqrt(3)` =1.732 ]
As observed form the top of a lighthouse, 100m above sea level, the angle of depression of a ship, sailing directly towards it, changes from 30° and 60° . Determine the distance travelled by the ship during the period of observation.
A kite is flying at a height of 60 m above the ground. The string attached to the kite is tied at the ground. It makes an angle of 60° with the ground. Assuming that the string is straight, find the length of the string.
The height of the vertical pole is \[\sqrt{3}\] times the length of its shadow on the ground, then angle of elevation of the sun at that time is
Find the angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of a tower of height `10sqrt(3)` m
