Advertisements
Advertisements
Question
As observed form the top of a lighthouse, 100m above sea level, the angle of depression of a ship, sailing directly towards it, changes from 30° and 60° . Determine the distance travelled by the ship during the period of observation.
Solution
Let OA be the lighthouse and B and C be the positions of the ship.
Thus, we have:
OA = 100m, ∠OBA = 30° and ∠OCA = 60°
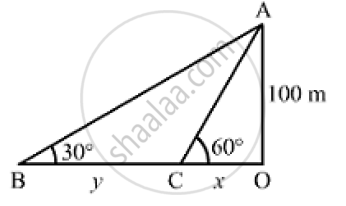
Let
OC = xmand BC = ym
In the right ΔOAC,we have
`(OA)/(OC) = tan 60° = sqrt(3) `
`⇒100/x = sqrt(3)`
`⇒ x = 100/sqrt(3) m`
Now, in the right ΔOBA,we have:
`(OA)/(OB) =tan 30° = 1/ sqrt(3)`
`⇒ 100/(x+y) = 1/ sqrt(3)`
`⇒ x+ y = 100 sqrt(3) `
On putting `x = 100/ sqrt(3)` in the above equation, we get:
`y = 100 sqrt(3) - 100/sqrt(3) = (300-100)/ sqrt(3) = 200/sqrt(3) = 115.47 m`
∴Distance travelled by the ship during the period of observation = B = y =115.47m
APPEARS IN
RELATED QUESTIONS
The angle of elevation of the top Q of a vertical tower PQ from a point X on the ground is 60°. From a point Y, 40 m vertically above X, the angle of elevation of the top Q of tower is 45. Find the height of the tower PQ and the distance PX. (Use `sqrt3=1.73)`
The angle of elevation of the top of a vertical tower PQ from a point X on the ground is 60°. At a point Y, 40 m vertically above X, the angle of elevation of the top is 45°. Calculate the height of the tower.
The angle of elevation of a stationary cloud from a point 2500 m above a lake is 15° and the angle of depression of its reflection in the lake is 45°. What is the height of the cloud above the lake level? (Use tan 15° = 0.268)
The angles of elevation of the top of a tower from two points at distance of 5 metres and 20 metres from the base of the tower and is the same straight line with it, are complementary. Find the height of the tower.
A vertical tower stands on a horizontal plane and is surmounted by a flagstaff of height 5 m. From a point on the ground the angles of elevation of the top and bottom of the flagstaff are 60° and 30° respectively. Find the height of the tower and the distance of the point from the tower. (take\[\sqrt{3}\]= 1.732)
From the top of the tower h metre high , the angles of depression of two objects , which are in the line with the foot of the tower are ∝ and ß (ß> ∝ ) cts .
A tree is broken by the wind. The top struck the ground at an angle of 30° and at a distance 30 m from the root. Find the whole height of the tree. (`sqrt(3)`=1.73)
The angle of elevation of the top of a cell phone tower from the foot of a high apartment is 60° and the angle of depression of the foot of the tower from the top of the apartment is 30°. If the height of the apartment is 50 m, find the height of the cell phone tower. According to radiation control norms, the minimum height of a cell phone tower should be 120 m. State if the height of the above mentioned cell phone tower meets the radiation norms
Two poles are 25 m and 15 m high, and the line joining their tops makes an angle of 45° with the horizontal. The distance between these poles is ______.
A boy 1.7 m tall is standing on a horizontal ground, 50 m away from a building. The angle of elevation of the top of the building from his eye is 60°. Calculate the height of the building. (Take `sqrt(3)` = 1.73)
