Advertisements
Advertisements
Question
From a point on a bridge across a river, the angles of depression of the banks on opposite sides of the river are 30° and 45° respectively. If the bridge is at a height of 2.5m from the banks, find the width of the river.
Solution
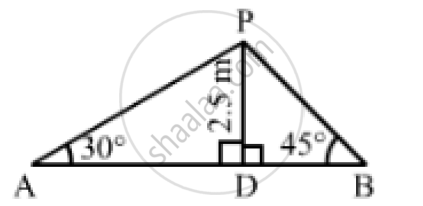
Let A and B be two points on the banks on the opposite side of the river and P be the point on the bridge at a height of 2.5 m.
Thus, we have:
DP = 2.5, ∠PAD = 30° and ∠PBD = 45°
In the right ΔAPD,we have:
`(DP)/(AD) = tan 30° = 1/sqrt(3)`
`⇒ 2.5 /(AD) = 1/ sqrt(3)`
`⇒ AD = 2.5 sqrt(3) m`
In the right ΔPDB,we have:
`(DP)/(BD) = tan 45° = 1`
`⇒ 2.5/(BD) = 1`
⇒ BD=2.5m
`∴"Width of the river" = AB = ( AD+ BD) =(2.5sqrt(3) + 2.5) = 6.83m`
APPEARS IN
RELATED QUESTIONS
The angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m from the base of the tower and in the same straight line with it are 60° and 30° respectively. Find the height of the tower.
The altitude of the sun at any instant is 60º. Find the height of the vertical pole that will cast a shadow of 30 m.
The angle of elevation of a tower from a point on the same level as the foot of the tower is 30°. On advancing 150 metres towards the foot of the tower, the angle of elevation of the tower becomes 60°. Show that the height of the tower is 129.9 metres (Use `sqrt3 = 1.732`)
The angle of elevation on the top of a building from the foot of a tower is 30° . The angle of elevation of the top of the tower when seen from the top of the second water is 60° .If the tower is 60m high, find the height of the building.

Radii of the top and the base of a frustum of a cone are 5 cm and 2 cm respectively. Its height is 9 cm. Find its volume. (π = 3.14)
An observer , 1.7 m tall , is` 20 sqrt3` m away from a tower . The angle of elevation from the eye of an observer to the top of tower is 300 . Find the height of the tower.
A man in a boat rowing away from a lighthouse 100 m high takes 2 minutes to change the angle of elevation of the top of the lighthouse from 60° to 30°.
Find the speed of the boat in metres per minute. [Use `sqrt(3` = 1.732]Use 3=1.732">
Find the angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of a tower of height `10sqrt(3)` m
The angle of elevation of the top of a tower from two points distant s and t from its foot are complementary. Prove that the height of the tower is `sqrt(st)`
Find the length of the shadow on the ground of a pole of height 18m when angle of elevation θ of the sun is such that tan θ = `6/7`.
