Advertisements
Advertisements
Question
The angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m from the base of the tower and in the same straight line with it are 60° and 30° respectively. Find the height of the tower.
Solution
Let the height of the tower be h m.
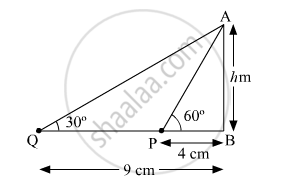
In ∆ABP,
`tan60^@ = h/4`
`=>sqrt3=h/4`
⇒h=1.73×4=6.92 cm
In ∆ABQ
`tan30^@=h/9`
`=>1/sqrt3=h/9`
`=>h=9/sqrt3cm= 5.20 cm`
Using the given data, we are getting two different values of h, which is not possible.
APPEARS IN
RELATED QUESTIONS
A balloon is connected to a meteorological station by a cable of length 200 m, inclined at 60º to the horizontal. Find the height of the balloon from the ground. Assume that there is no slack in the cable
A balloon of radius γ makes an angle α at the eye of an observer and the angle of elevation of its centre is β. Then find the height of its centre from the ground level
The horizontal distance between two trees of different heights is 60 m. The angle of depression of the top of the first tree, when seen from the top of the second tree, is 45°. If the height of the second tree is 80 m, find the height of the first tree.
It is found that on walking x meters towards a chimney in a horizontal line through its base, the elevation of its top changes from 30° to 60°. The height of the chimney is
Find the angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of a tower of height `10sqrt(3)` m
From the top of the tower 60 m high the angles of depression of the top and bottom of a vertical lamp post are observed to be 38° and 60° respectively. Find the height of the lamp post (tan 38° = 0.7813, `sqrt(3)` = 1.732)
In given figure, the value of AE is ____________.
A ladder 15 metres long just reaches the top of a vertical wall. If the ladder makes an angle of 60° with the wall, find the height of the wall.
From a point on a bridge across a river, the angles of depression of the banks on opposite sides of the river are 30° and 45° respectively. If the bridge is at a height of 3 m from the banks, find the width of the river. (Use `sqrt(3)` = 1.73)
Read the following passage:
A boy is standing on the top of light house. He observed that boat P and boat Q are approaching the light house from opposite directions. He finds that angle of depression of boat P is 45° and angle of depression of boat Q is 30°. He also knows that height of the light house is 100 m.
|
Based on the above information, answer the following questions.
- What is the measure of ∠APD?
- If ∠YAQ = 30°, then ∠AQD is also 30°, Why?
- Find length of PD
OR
Find length of DQ


