Advertisements
Advertisements
Question
The horizontal distance between two trees of different heights is 60 m. The angle of depression of the top of the first tree, when seen from the top of the second tree, is 45°. If the height of the second tree is 80 m, find the height of the first tree.
Solution
Let the difference between two trees be DE = 60 m and angle of depression of the first tree from the top to the top of the second tree is ∠ABC = 45°.
Let BE = H m, AC = h m, AD = 80m.
We have to find the height of the first tree
The corresponding figure is as follows
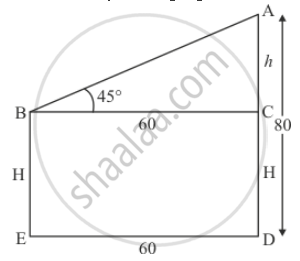
In ΔABC
`=> tan B = (AC)/(BC)`
`=> tan 45° = h/60`
`=> 1 - h/60`
`=> h = 60`
Since H = 80 - h
=> H = 80 - 60
=> H = 20
Hence the heght of first tree is 20 m
APPEARS IN
RELATED QUESTIONS
A 1.5 m tall boy is standing at some distance from a 30 m tall building. The angle of elevation from his eyes to the top of the building increases from 30° to 60° as he walks towards the building. Find the distance he walked towards the building.
A tower stands vertically on the ground. From a point on the ground, 20 m away from the foot of the tower, the angle of elevation of the top of the tower is 600. What is the height of the tower?
From the top of a tower of height 50 m, the angles of depression of the top and bottom of a pole are 30° and 45° respectively. Find
(i) how far the pole is from the bottom of a tower,
(ii) the height of the pole. (Use \[\sqrt{3} = 1 . 732\])
A solid right-circular cone of height 60 cm and radius 30 cm is dropped in a right-circular cylinder full of water of height 180 cm and radius 60 cm. Find the volume of water left in the cylinder, in cubic metres ?
From the top of a rock `50sqrt(3)` m high, the angle of depression of a car on the ground is observed to be 30°. Find the distance of the car from the rock
The angles of elevation of the top of a tower from two points distant s and t from its foot are complementary. Then the height of the tower is ____________.
The shadow of a tower standing on a level plane is found to be 50 m longer when Sun’s elevation is 30° than when it is 60°. Then the height of the tower is ____________.
We all have seen the airplanes flying in the sky but might have not thought of how they actually reach the correct destination. Air Traffic Control (ATC) is a service provided by ground-based air traffic controllers who direct aircraft on the ground and through a given section of controlled airspace, and can provide advisory services to aircraft in non-controlled airspace. Actually, all this air traffic is managed and regulated by using various concepts based on coordinate geometry and trigonometry.
At a given instance, ATC finds that the angle of elevation of an airplane from a point on the ground is 60°. After a flight of 30 seconds, it is observed that the angle of elevation changes to 30°. The height of the plane remains constantly as `3000sqrt(3)` m. Use the above information to answer the questions that follow-
- Draw a neat labelled figure to show the above situation diagrammatically.
- What is the distance travelled by the plane in 30 seconds?
OR
Keeping the height constant, during the above flight, it was observed that after `15(sqrt(3) - 1)` seconds, the angle of elevation changed to 45°. How much is the distance travelled in that duration. - What is the speed of the plane in km/hr.
The angle of elevation of the top P of a vertical tower PQ of height 10 from a point A on the horizontal ground is 45°. Let R be a point on AQ and from a point B, vertically above R, the angle of elevation of P is 60°. If ∠BAQ = 30°, AB = d and the area of the trapezium PQRB is α, then the ordered pair (d, α) is ______.
A straight highway leads to the foot of a tower. A man standing on the top of the 75 m high tower observes two cars at angles of depression of 30° and 60°, which are approaching the foot of the tower. If one car is exactly behind the other on the same side of the tower, find the distance between the two cars. (use `sqrt(3)` = 1.73)
