Advertisements
Advertisements
Question
A tree standing on a horizontal plane is leaning towards the east. At two points situated at distances a and b exactly due west on it, the angles of elevation of the top are respectively α and β. Prove that the height of the top from the ground is `((b - a)tan alpha tan beta)/(tan alpha - tan beta)`
Solution
Let OP be the tree and A, B be the two points such OA = a and OB = b and angle of elevation to the tops are α and β respectively.
Let OL = x and PL = h
We have to prove the following
`h = ((b - a)tan alpha tan beta)/(tan alpha - tan beta)`
The corresponding figure is as follows
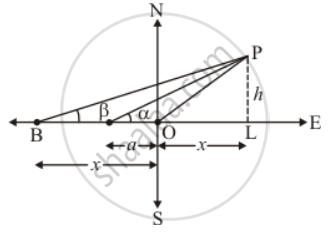
In ΔALP
`=> tan alpha = (PL)/(OA + OL)`
`=> tan alpha = h/(a + x)`
`=> 1/(cot alpha) = h/(a + x)`
`=> h cot alpha = a + x`.....(1)
Again in ΔBLP
`=> tan beta = (PL)/(OB + OL)`
`=> tan beta = h/(b + x)`
`=> 1/(cot beta) = h/(b + x)`
`=> h cot beta = b + x` .....(2)
Subtracting equation (1) from (2) we get
`=> h cot beta - hcot alpha = b - a`
`=> h(cot beta - cot alpha) = b - a`
`=> h (b -a)/(cot beta - cot alpha)`
`h = ((b - a)tan alpha tan beta)/(tan alpha - tan beta)`
Hence height of the top from ground is `h = ((b -a) tan alpha tan beta)/((tan alpha - tan beta))`
APPEARS IN
RELATED QUESTIONS
At a point A, 20 metres above the level of water in a lake, the angle of elevation of a cloud is 30˚. The angle of depression of the reflection of the cloud in the lake, at A is 60˚.
Find the distance of the cloud from A.
A contractor plans to install two slides for the children to play in a park. For the children below the age of 5 years, she prefers to have a slide whose top is at a height of 1.5 m, and is inclined at an angle of 30° to the ground, where as for the elder children, she wants to have a steep side at a height of 3 m, and inclined at an angle of 60° to the ground. What should be the length of the slide in each case?
A person is standing at a distance of 80 m from a church looking at its top. The angle of elevation is of 45°. Find the height of the church.
If the angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m from the base of the tower in the same straight line with it are complementary, find the height of the tower.
An observer, 1.5 m tall, is 28.5 m away from a 30 m high tower. Determine the angle of elevation of the top of the tower from the eye of the observer.
A statue 1.6 m tall stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the statue is 60ϒ and from the same point the angle of elevation of the top of the pedestal is 40ϒ. Find the height of the pedestal. (tan 40° = 0.8391, `sqrt(3)` = 1.732)
In given figure, the value of ZC is ____________.
In figure given ABCD is a rectangle, the value of CE is ____________.

A plane is observed to be approaching the airport. It is at a distance of 12 km from the point of observation and makes an angle of elevation of 60°. The height above the ground of the plane is ____________.
The shadow of a tower standing on a level plane is found to be 50 m longer when Sun’s elevation is 30° than when it is 60°. Then the height of the tower is ____________.
