Advertisements
Advertisements
प्रश्न
A tree standing on a horizontal plane is leaning towards the east. At two points situated at distances a and b exactly due west on it, the angles of elevation of the top are respectively α and β. Prove that the height of the top from the ground is `((b - a)tan alpha tan beta)/(tan alpha - tan beta)`
उत्तर
Let OP be the tree and A, B be the two points such OA = a and OB = b and angle of elevation to the tops are α and β respectively.
Let OL = x and PL = h
We have to prove the following
`h = ((b - a)tan alpha tan beta)/(tan alpha - tan beta)`
The corresponding figure is as follows
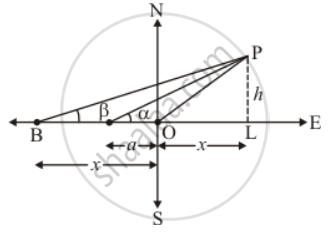
In ΔALP
`=> tan alpha = (PL)/(OA + OL)`
`=> tan alpha = h/(a + x)`
`=> 1/(cot alpha) = h/(a + x)`
`=> h cot alpha = a + x`.....(1)
Again in ΔBLP
`=> tan beta = (PL)/(OB + OL)`
`=> tan beta = h/(b + x)`
`=> 1/(cot beta) = h/(b + x)`
`=> h cot beta = b + x` .....(2)
Subtracting equation (1) from (2) we get
`=> h cot beta - hcot alpha = b - a`
`=> h(cot beta - cot alpha) = b - a`
`=> h (b -a)/(cot beta - cot alpha)`
`h = ((b - a)tan alpha tan beta)/(tan alpha - tan beta)`
Hence height of the top from ground is `h = ((b -a) tan alpha tan beta)/((tan alpha - tan beta))`
APPEARS IN
संबंधित प्रश्न
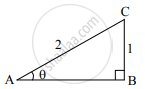
In the following figure, in ΔABC, BC = 1, AC = 2, ∠B = 90°. Find the value of sin θ.
A ladder is placed along a wall of a house such that its upper end is touching the top of the wall. The foot of the ladder is 2 m away from the wall and the ladder is making an angle of 60° with the level of the ground. Determine the height of the wall.
From the top of a 15 m high building, the angle of elevation of the top of a tower is found to be 30°. From the bottom of the same building, the angle of elevation of the top of the tower is found to be 60°. Find the height of the tower and the distance between tower and the building.
An observer, 1.5 m tall, is 28.5 m away from a tower 30 m high. Determine the angle of elevation of the top of the tower from his eye.
A ladder 15 m long makes an angle of 60° with the wall. Find the height of the point where the ladder touches the wall.
A pole casts a shadow of length \[2\sqrt{3}\] m on the ground, when the sun's elevation is 60°. Find the height of the pole.
An observer, 1.5 m tall, is 28.5 m away from a 30 m high tower. Determine the angle of elevation of the top of the tower from the eye of the observer.
The angles of elevation of the top of the rock from the top and foot of 100 m high tower are respectively 30° and 45°. The height of the rock is ____________.
A statue, 2 m tall, stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the statue is 60° and from the same point, the angle of elevation of the top of the pedestal is 45°. Find the height of the pedestal.
If the height of the tower is equal to the length of its shadow, then the angle of elevation of the sun is ______.
