Advertisements
Advertisements
Question
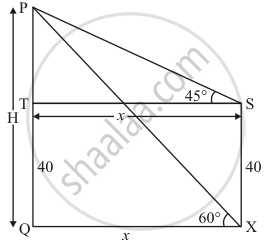
The angle of elevation of the top of a vertical tower PQ from a point X on the ground is 60°. At a point Y, 40 m vertically above X, the angle of elevation of the top is 45°. Calculate the height of the tower.
Solution
Let PQ be the tower of height H m and an angle of elevation of the top of tower PQ from point X is 60°. An angle of elevation at 40 m vertical from point X is 45°.
Let PQ = H m and SX = 40m. OX = x, ∠PST = 45°, ∠PXQ = 60°
Here we have to find height of tower.
The corresponding figure is as follows
We use trigonometric ratios.
In ΔPST
`=> tan 45^@ = h/x`
`=> 1 = h/x`
`=> x = h`
Again in ΔPST
`=> tan 456@ = h/x`
`=> 1 = h/x`
`=> x = h`
Again in ΔPXQ
`=> tan 60^@ = (h + 40)/x`
`=> sqrt3 = (h + 40)/x`
`=> h + 40 = sqrt3h`
`=> h(sqrt3 - ) = 40`
`=> h = 40/(sqrt3 - 1)`
`=> h = 54.64`
Therefore `H = 54.64 + 40`
`=> H = 94.64`
Hence the height of tower uis 94.64 m
APPEARS IN
RELATED QUESTIONS
From a point on the ground 40 m away from the foot of a tower, the angle of elevation of the top of the tower is 30º. The angle of elevation of the top of a water tank (on the top of the tower) is 45º. Find the (i) height of the tower (ii) the depth of the tank.
An aeroplane is flying at a height of 300 m above the ground. Flying at this height, the angles of depression from the aeroplane of two points on both banks of a river in opposite directions are 45° and 60° respectively. Find the width of the river. [Use `sqrt3` = 1⋅732]
A man standing on the deck of a ship, which is 8 m above water level. He observes the angle of elevation of the top of a hill as 60° and the angle of depression of the base of the hill as 30°. Calculate the distance of the hill from the ship and the height of the hill.
From the top of a building AB, 60 m high, the angles of depression of the top and bottom of a vertical lamp post CD are observed to be 30° and 60° respectively. Find
1) the horizontal distance between AB and CD
2) the height of the lamp post.
3) the difference between the heights of the building and the lamp post.
The angle of elevation of the top of a tower standing on a horizontal plane from a point A is α. After walking a distance d towards the foot of the tower the angle of elevation is found to be β. The height of the tower is
It is found that on walking x meters towards a chimney in a horizontal line through its base, the elevation of its top changes from 30° to 60°. The height of the chimney is
The height of the vertical pole is \[\sqrt{3}\] times the length of its shadow on the ground, then angle of elevation of the sun at that time is
Two persons are standing ‘x’ metres apart from each other and the height of the first person is double that of the other. If from the middle point of the line joining their feet an observer finds the angular elevations of their tops to be complementary, then the height of the shorter person (in metres) is
The angle of elevation of a cloud from a point h metres above a lake is β. The angle of depression of its reflection in the lake is 45°. The height of location of the cloud from the lake is
The top of a hill when observed from the top and bottom of a building of height h is at angles of elevation p and q respectively. What is the height of the hill?
