Advertisements
Advertisements
Question
Two persons are standing ‘x’ metres apart from each other and the height of the first person is double that of the other. If from the middle point of the line joining their feet an observer finds the angular elevations of their tops to be complementary, then the height of the shorter person (in metres) is
Options
`sqrt(2)x`
`x/(2sqrt(2))`
`x/sqrt(2)`
2x
Solution
`x/(2sqrt(2))`
Explanation;
Hint:
Consider the height of the 2nd person ED be h
Height of the second person is 2h
C is the midpoint of BD
In the right ∆ABC, tan θ = `"AB"/"BC"`
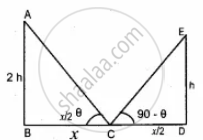
tan θ = `(2"h")/(x/2) = (4"h")/x` ...(1)
In the right ΔDCE,
tan (90 − θ) = `"ED"/"CD" = "h"/(x/2)`
cot θ = `(2"h")/x`
⇒ `1/tan theta = (2"h")/x`
tan θ = `x/(2"h")` ...(2)
From (1) and (2) we get,
`(4"h")/x = x/(2"h")`
x2 = 8h2
⇒ h2 = `x^2/8`
h = `sqrt(x^2/8)`
= `x 1/sqrt(4 xx 2)`
= `x/(2sqrt(2))`
APPEARS IN
RELATED QUESTIONS
A ladder against a vertical wall makes an angle of 45º with the ground. The foot of the ladder is 3m from the wall. Find the length of the ladder
From the top of a cliff 25 m high the angle of elevation of a tower is found to be equal to the angle of depression of the foot of the tower. Find the height of the tower
An observer finds the angle of elevation of the top of the tower from a certain point on the ground as 30°. If the observe moves 20 m towards the base of the tower, the angle of elevation of the top increases by 15°, find the height of the tower.
An aeroplane flying horizontally 1 km above the ground is observed at an elevation of 60°. After 10 seconds, its elevation is observed to be 30°. Find the speed of the aeroplane in km/hr.
From the top of a tower of height 50 m, the angles of depression of the top and bottom of a pole are 30° and 45° respectively. Find
(i) how far the pole is from the bottom of a tower,
(ii) the height of the pole. (Use \[\sqrt{3} = 1 . 732\])
A storm broke a tree and the treetop rested 20 m from the base of the tree, making an angle of 60° with the horizontal. Find the height of the tree.
If the angles of elevation of the top of a tower from two points distant a and b from the base and in the same straight line with it are complementary, then the height of the tower is
A bird is sitting on the top of a 80 m high tree. From a point on the ground, the angle of elevation of the bird is 45°. The bird flies away horizontally in such away that it remained at a constant height from the ground. After 2 seconds, the angle of elevation of the bird from the same point is 30°. Determine the speed at which the bird flies `(sqrt(3) = 1.732)`
A TV tower stands vertically on a bank of a canal, with a height of `10 sqrt3` m. From a point on the other bank directly opposite the tower, the angle of elevation of the top of the tower is 60°. From another point on the line joining this point to the foot of the tower, the angle of elevation of the top of the tower is 30°. Find the distance between the opposite bank of the canal and the point with a 30° angle of elevation.
The angles of depression of two objects from the top of a 100 m hill lying to its east are found to be 45° and 30°. Find the distance between the two objects. (Take `sqrt3 = 1.73`)
