Advertisements
Advertisements
Question
A bird is sitting on the top of a 80 m high tree. From a point on the ground, the angle of elevation of the bird is 45°. The bird flies away horizontally in such away that it remained at a constant height from the ground. After 2 seconds, the angle of elevation of the bird from the same point is 30°. Determine the speed at which the bird flies `(sqrt(3) = 1.732)`
Solution
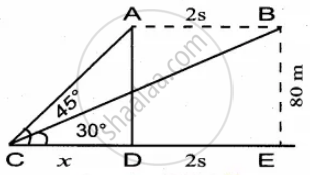
A is the initial position of the bird B is the final position of the bird Let the speed of the bird be s
Distance = speed × time
∴ AB = 2x
Let CD be x
∴ CE = x + 2s
In the ∆CDA, tan 45° = `"AD"/"CD"`
1 = `80/x`
x = 80 ...(1)
In the ∆BCE
tan 30° = `"BE"/"CE"`
`1/sqrt(3) = 80/(x + 2"s")`
x + 2s = `80sqrt(3)`
x = `80sqrt(3) - 2"s"` ...(2)
From (1) and (2) we get
`80 sqrt(3) - 2"s"` = 80
`80 sqrt(3) - 80` = 2s
⇒ `80(sqrt(3) - 1)` = 2s
s = `(80(sqrt(3) - 1))/2`
= 40(1.732 – 1)
= 40 × 0.732
= 29.28
Speed of the flying bird = 29.28 m/sec
APPEARS IN
RELATED QUESTIONS
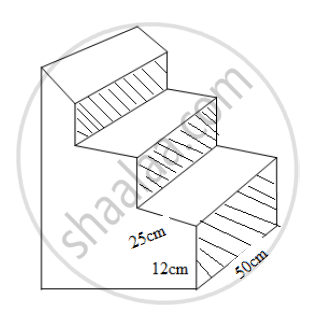
There are three stair-steps as shown in the figure below. Each stair step has width 25 cm, height 12 cm and length 50 cm. How many bricks have been used in it, if each brick is 12.5 cm x 6.25 cm x 4 cm?
The angle of depression of a car parked on the road from the top of a 150 m high tower is 30°. The distance of the car from the tower (in metres) is
`(A) 50sqrt3`
`(B) 150sqrt 3`
`(C) 150sqrt2`
`(D) 75`
If a vertical pole 6m high has a shadow of length 2 √3 metres, find the angle of elevation of the sun.
The angle of elevation of a stationary cloud from a point 2500 m above a lake is 15° and the angle of depression of its reflection in the lake is 45°. What is the height of the cloud above the lake level? (Use tan 15° = 0.268)
A boy is standing on the ground and flying a kite with 100 m of string at an elevation of 30°. Another boy is sanding on the roof of a 10 m high building and is flying his kite at an elevation of 45°. Both the boys are on opposite sides of both the kites. Find the length of the string that the second boy must have so that the two kites meet.
An observer, 1.5 m tall, is 28.5 m away from a 30 m high tower. Determine the angle of elevation of the top of the tower from the eye of the observer.
Three villagers A, B and C can see each other using telescope across a valley. The horizontal distance between A and B is 8 km and the horizontal distance between B and C is 12 km. The angle of depression of B from A is 20° and the angle of elevation of C from B is 30°. Calculate the vertical height between B and C. (tan 20° = 0.3640, `sqrt3` = 1.732)

The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 60 m high, find the height of the building.
The angle of elevation of the top of a vertical tower from a point on the ground is 60°. From another point 10 m vertically above the first, its angle of elevation is 45°. Find the height of the tower.
In the given figure, AB is tower of height 50 m. A man standing on its top, observes two car on the opposite sides of the tower with angles of depression 30° and 45° respectively. Find the distance between the two cars.

