Advertisements
Advertisements
Question
An aeroplane is flying parallel to the Earth’s surface at a speed of 175 m/sec and at a height of 600 m. The angle of elevation of the aeroplane from a point on the Earth’s surface is 37°. After what period of time does the angle of elevation increase to 53°? (tan 53° = 1.3270, tan 37° = 0.7536)
Solution
Let C is the initial and D is the final position of the aeroplane.
Let the time taken by the aeroplane be t
∴ CD = 175 t ...(Distance = speed × time)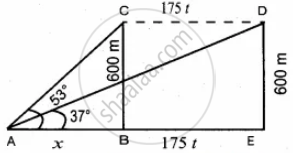
Let AB be x
∴ AE = x + 175 t
In the right ∆ABC
tan 53° = `"BC"/"AB"`
⇒ 1.3270 = `600/x`
x = `600/1.327` ...(1)
In the right ΔAED, tan 37° = `"DE"/"AE"`
0.7536 = `600/(x + 175"t")`
x + 175 t = `600/(0.7536)`
x = `600/(0.7536) - 175"t"` ...(2)
From (1) and (2) we get
`600/(1.327) = 600/(0.7536) - 175"t"`
175 t = `600/(0.7536) - 600/(1.327)`
175 t = 796.18 − 452.15 = 344.03
∴ t = `(344.03)/175` = 1.97 seconds
∴ Time taken is 1.97 seconds
APPEARS IN
RELATED QUESTIONS
The length of a string between a kite and a point on the ground is 90 meters. If the string makes an angle O with the ground level such that tan O = 15/8, how high is the kite? Assume that there is no slack in the string.
From the point of a tower 100m high, a man observe two cars on the opposite sides to the tower with angles of depression 30° and 45 respectively. Find the distance between the cars
Two buildings are facing each other on a road of width 12 metre. From the top of the first building, which is 10 metre high, the angle of elevation of the top of the second is found to be 60°. What is the height of the second building ?
In given figure, the value of ZC is ____________.
The angles of depression of the top and the bottom of a 10 m tall building from the top of a multi-storeyed building are 30° and 45°, respectively. Find the height of the multi-storeyed building.
The angle of elevation of the top of a tower from a certain point is 30°. If the observer moves 20 meters towards the tower, the angle of elevation of the top increases by 15°. Find the height of the tower ____________.
An observer 1.5 metres tall is 20.5 metres away from a tower 22 metres high. Determine the angle of elevation of the top of the tower from the eye of the observer.
The angle of elevation of the top of a tower from two points distant s and t from its foot are complementary. Prove that the height of the tower is `sqrt(st)`
The top of a banquet hall has an angle of elevation of 45° from the foot of a transmission tower and the angle of elevation of the topmost point of the tower from the foot of the banquet hall is 60°. If the tower is 60 m high, find the height of the banquet hall in decimals.
A straight highway leads to the foot of a tower. A man standing on the top of the 75 m high tower observes two cars at angles of depression of 30° and 60°, which are approaching the foot of the tower. If one car is exactly behind the other on the same side of the tower, find the distance between the two cars. (use `sqrt(3)` = 1.73)
