Advertisements
Advertisements
Question
An observer 1.5 metres tall is 20.5 metres away from a tower 22 metres high. Determine the angle of elevation of the top of the tower from the eye of the observer.
Solution
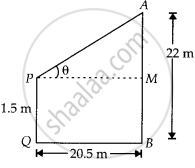
Let the angle of elevation of the top of the tower from the eye of the observer is θ
Given that,
AB = 22 m,
PQ = 1.5 m = MB
And QB = PM = 20.5 m
⇒ AM = AB – MB
= 22 – 1.5
= 20.5 m
Now, In ∆APM,
tan θ = `"AM"/"PM" = 20.5/20.5` = 1
⇒ tan θ = tan 45°
∴ θ = 45°
Hence, the required angle of elevation of the top of the tower from the eye of the observer is 45°.
APPEARS IN
RELATED QUESTIONS
An aeroplane is flying at a height of 300 m above the ground. Flying at this height, the angles of depression from the aeroplane of two points on both banks of a river in opposite directions are 45° and 60° respectively. Find the width of the river. [Use `sqrt3` = 1⋅732]
A man on the deck of a ship is 10 m above the water level. He observes that the angle of elevation of the top of a cliff is 45° and the angle of depression of the base is 300. Calculate the distance of the cliff from the ship and the height of the cliff.
An observer, 1.5 m tall, is 28.5 m away from a tower 30 m high. Determine the angle of elevation of the top of the tower from his eye.
A pole casts a shadow of length \[2\sqrt{3}\] m on the ground, when the sun's elevation is 60°. Find the height of the pole.
A tower stands vertically on the ground. From a point on the ground which is 25 m away from the foot of the tower, the angle of elevation of the top of the tower is found to be 45°. Then the height (in meters) of the tower is
Three villagers A, B and C can see each other using telescope across a valley. The horizontal distance between A and B is 8 km and the horizontal distance between B and C is 12 km. The angle of depression of B from A is 20° and the angle of elevation of C from B is 30°. Calculate the vertical height between A and B. (tan 20° = 0.3640, `sqrt3` = 1.732)

An observer 1.5 m tall is 28.5 m away from a tower. The angle of elevation of the top of the tower from her eyes is 45°. What is the height of the tower?
The angle of elevation of the top of a tower from a certain point is 30°. If the observer moves 20 meters towards the tower, the angle of elevation of the top increases by 15°. Find the height of the tower ____________.
An aeroplane when flying at a height of 3125 m from the ground passes vertically below another plane at an instant when the angles of elevation of the two planes from the same point on the ground are 30° and 60° respectively. Find the distance between the two planes at that instant.
Read the following passage:
|
Radio towers are used for transmitting a range of communication services including radio and television. The tower will either act as an antenna itself or support one or more antennas on its structure; On a similar concept, a radio station tower was built in two Sections A and B. Tower is supported by wires from a point O. Distance between the base of the tower and point O is 36 cm. From point O, the angle of elevation of the top of the Section B is 30° and the angle of elevation of the top of Section A is 45°.
|
Based on the above information, answer the following questions:
- Find the length of the wire from the point O to the top of Section B.
- Find the distance AB.
OR
Find the area of ∠OPB. - Find the height of the Section A from the base of the tower.

