Advertisements
Advertisements
Question
A man on the deck of a ship is 10 m above the water level. He observes that the angle of elevation of the top of a cliff is 45° and the angle of depression of the base is 300. Calculate the distance of the cliff from the ship and the height of the cliff.
Solution
Let H be the height of the cliff CE. And a man is standing on the ships at the height of 10 meters above from the water level.
Let AB = 10, BC = x, AD = BC, AB = DC, DE = h.
∠ACB = 30° and ∠DAE = 45°
We have tofind H and xT
The corresponding figure is as follows
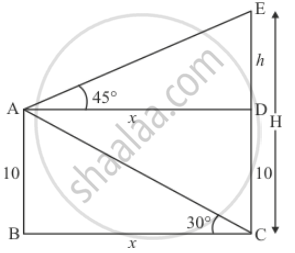
In Δ ABC
`=> tan C = (AB)/(BC)`
`=> tan 30^@ = = 10/x`
`=> 1/sqrt3 = 10/x`
`=> x = 10sqrt3`
Again in ΔDAE
`=> tan A = (DE)/(AD)`
`=> tan 45^@ = h/x`
`=> 1 = h/x`
=> x = h
`=> x = 10sqrt3`
Therefore H = h + 10
`=> H = 10sqrt3 + 10`
`=> H = 10(sqrt3 + 1)`
`=> H = 27.32`
Hence the required distance is `10sqrt3` and height is 27.32 m
APPEARS IN
RELATED QUESTIONS
There is a small island in the middle of a 100 m wide river and a tall tree stands on the island. P and Q are points directly opposite to each other on two banks, and in line with the tree. If the angles of elevation of the top of the tree from P and Q are respectively 30º and 45º, find the height of the tree. (Use `sqrt(3)` = 1.732)
A statue, 1.6 m tall, stands on a top of pedestal, from a point on the ground, the angle of elevation of the top of statue is 60° and from the same point the angle of elevation of the top of the pedestal is 45°. Find the height of the pedestal.
The angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m. from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is 6 m.
From a point P on the ground the angle of elevation of a 10 m tall building is 30°. A flag is hoisted at the top of the building and the angle of elevation of the top of the flag-staff from P is 45°. Find the length of the flag-staff and the distance of the building from the point P. (Take `sqrt3` = 1.732)
PQ is a post of given height a, and AB is a tower at some distance. If α and β are the angles of elevation of B, the top of the tower, at P and Q respectively. Find the height of the tower and its distance from the post.
An electrician has to repair an electric fault on a pole of height 4 meters. He needs to reach a point 1 meter below the top of the pole to undertake the repair work. What should be the length of the ladder that he should use, which when inclined at an angle of 60° to the horizontal would enable him to reach the required position?
The line drawn from the eye of an observer to the point in the object viewed by the observer is known as ____________.
As observed from the top of a 150 m high lighthouse from the sea level, the angles of depression of the two ships are 30° and 45°. If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships.
The angles of depression of two objects from the top of a 100 m hill lying to its east are found to be 45° and 30°. Find the distance between the two objects. (Take `sqrt3 = 1.73`)
If the height of the tower is equal to the length of its shadow, then the angle of elevation of the sun is ______.
