Advertisements
Advertisements
प्रश्न
A man on the deck of a ship is 10 m above the water level. He observes that the angle of elevation of the top of a cliff is 45° and the angle of depression of the base is 300. Calculate the distance of the cliff from the ship and the height of the cliff.
उत्तर
Let H be the height of the cliff CE. And a man is standing on the ships at the height of 10 meters above from the water level.
Let AB = 10, BC = x, AD = BC, AB = DC, DE = h.
∠ACB = 30° and ∠DAE = 45°
We have tofind H and xT
The corresponding figure is as follows
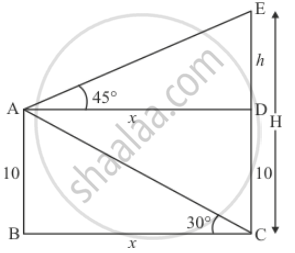
In Δ ABC
`=> tan C = (AB)/(BC)`
`=> tan 30^@ = = 10/x`
`=> 1/sqrt3 = 10/x`
`=> x = 10sqrt3`
Again in ΔDAE
`=> tan A = (DE)/(AD)`
`=> tan 45^@ = h/x`
`=> 1 = h/x`
=> x = h
`=> x = 10sqrt3`
Therefore H = h + 10
`=> H = 10sqrt3 + 10`
`=> H = 10(sqrt3 + 1)`
`=> H = 27.32`
Hence the required distance is `10sqrt3` and height is 27.32 m
APPEARS IN
संबंधित प्रश्न
A man observes a car from the top of a tower, which is moving towards the tower with a uniform speed. If the angle of depression of the car changes from 30° to 45° in 12 minutes, find the time taken by the car now to reach the tower.
The shadow of a tower, when the angle of elevation of the sun is 45°, is found to be 10 m. longer than when it was 600. Find the height of the tower.
From the top of a 15 m high building, the angle of elevation of the top of a tower is found to be 30°. From the bottom of the same building, the angle of elevation of the top of the tower is found to be 60°. Find the height of the tower and the distance between tower and the building.
Find the angle of elevation of the sum (sun's altitude) when the length of the shadow of a vertical pole is equal to its height.
An observer, 1.5 m tall, is 28.5 m away from a tower 30 m high. Determine the angle of elevation of the top of the tower from his eye.
Two poles of heights 18 metre and 7 metre are erected on a ground. The length of the wire fastened at their tops in 22 metre. Find the angle made by the wire with the horizontal.
AB is a pole of height 6 m standing at a point B and CD is a ladder inclined at angle of 600 to the horizontal and reaches upto a point D of pole . If AD = 2.54 m , find the length of the ladder.
It is found that on walking x meters towards a chimney in a horizontal line through its base, the elevation of its top changes from 30° to 60°. The height of the chimney is
In given figure, the value of ZC is ____________.
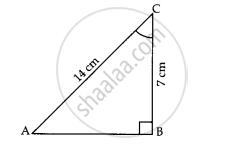
In given figure, AD = 4 cm, BD = 3 cm and CB = 12 cm. The value of tan `theta` is ____________.

