Advertisements
Advertisements
प्रश्न
A fire in a building B is reported on the telephone to two fire stations P and Q, 20 km apart from each other on a straight road. P observes that the fire is at an angle of 60° to the road and Q observes that it is at an angle of 45° to the road. Which station should send its team and how much will this team have to travel?
उत्तर
Let AB be the building of height h. P Observes that the fire is at an angle of 60° to the road and Q observes that the fire is at an angle of 45° to the road.
Let QA = x, AP = y. And `∠BPA = 60^@`,∠BQA = 45°, given PQ = 20.
Here clearly ∠APB > ∠AQB
=> ∠ABP < ∠ABQ
=> AP < AQ
So station P is near to the building. Hence station P must send its team
We sketch the following figure
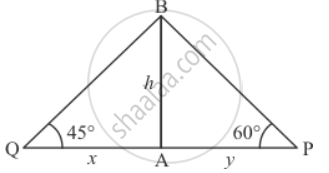
So we use trigonometric ratios.
In ΔPAB
`tan P = (AB)/(AP)`
`=> tan 60^@ = h/y`
`=> h = sqrt3y`
Again in ΔQAB
`=> tan Q = (AB)/(QA)`
`=> tan 45^@ = h/x`
`=> 1 = h/x`
`=> x = h`
Now
x + y = 20
`=> h + y = 20` [∵ x = h]
`=> sqrt3y + y = 20` [∵ `h = sqrt3y`]
`=> y = 20/(sqrt3 + 1) = 10(sqrt3 - 1)`
Hence the team from station P wil have to travel `10(sqrt3 - 1)` km
APPEARS IN
संबंधित प्रश्न
A vertical tower stands on a horizontal plane and is surmounted by a flagstaff of height 7m. At a point on the plane, the angle of elevation of the bottom of the flagstaff is 30º and that of the top of the flagstaff is 45º. Find the height of the tower.
A flag-staff stands on the top of a 5 m high tower. From a point on the ground, the angle of elevation of the top of the flag-staff is 60° and from the same point, the angle of elevation of the top of the tower is 45°. Find the height of the flag-staff.
A tower stands vertically on the ground. From a point on the ground which is 20 m away from the foot of the tower, the angle of elevation of its top is found to be 60°. Find the height of the tower. [Take `sqrt(3)` =1.732 ]
Two ships are approaching a light-house from opposite directions. The angles of depression of the two ships from the top of the light-house are 30° and 45°. If the distance between the two ships is 100 m, find the height of the light-house. \[[Use \sqrt{3} = 1 . 732]\]
A boy standing at a distance of 48 meters from a building observes the top of the building and makes an angle of elevation of 30°. Find the height of the building.
The height of the vertical pole is \[\sqrt{3}\] times the length of its shadow on the ground, then angle of elevation of the sun at that time is
An electrician has to repair an electric fault on a pole of height 4 m. He needs to reach a point 1.3 m below the top of the pole to undertake the repair work. What should be the length of the ladder that he should use which when inclined at an angle of 60° to the horizontal would enable him to reach the required position?
If a man standing on a platform 3 meters above the surface of a lake observes a cloud and its reflection in the lake, then calculate the angle of elevation of the cloud.
The angle of elevation of the top of a tower from certain point is 30°. If the observer moves 20 metres towards the tower, the angle of elevation of the top increases by 15°. Find the height of the tower.
An aeroplane when flying at a height of 3125 m from the ground passes vertically below another plane at an instant when the angles of elevation of the two planes from the same point on the ground are 30° and 60° respectively. Find the distance between the two planes at that instant.
