Advertisements
Advertisements
प्रश्न
The angle of elevation of the top of a tower from certain point is 30°. If the observer moves 20 metres towards the tower, the angle of elevation of the top increases by 15°. Find the height of the tower.
उत्तर
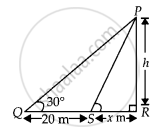
Let the height of the tower be h.
Also, SR = x m,
Given that, QS = 20 m
`sqrt("PQR")` = 30°
And `sqrt("PSR") = sqrt("PQR") + 15^circ`
= 30° + 15°
= 45°
Now, In ∆PSR,
tan 45° = `"PR"/"SR" = "h"/x`
⇒ `1 = "h"/x` ...[∵ tan 45° = 1]
⇒ x = h ...(i)
Now, In ∆PQR
tan 30° = `"PR"/"QR" = "PR"/("QS" + "SR")`
⇒ tan 30° = `"h"/(20 + x)`
⇒ 20 + x = `"h"/(tan 30^circ) = "h"/(1/sqrt(3))`
⇒ 20 + x = `"h"sqrt(3)`
⇒ 20 + h = `"h"sqrt(3)` ...[From (i)]
⇒ 20 = `"h"sqrt(3) - "h"`
⇒ `"h"(sqrt(3) - 1)` = 20
⇒ h = `20/(sqrt(3) - 1) * (sqrt(3) + 1)/(sqrt(3) + 1)` ...[By rationalisation]
⇒ h = `(20(sqrt(3) + 1))/(3 - 1) = (20(sqrt(3) + 1))/2`
⇒ h = `10(sqrt(3) + 1) "m"`
Hence, the required height of tower is `10(sqrt(3) + 1) "m"`.
APPEARS IN
संबंधित प्रश्न
If a vertical pole 6m high has a shadow of length 2 √3 metres, find the angle of elevation of the sun.
The angle of elevation of the top of a vertical tower PQ from a point X on the ground is 60°. At a point Y, 40 m vertically above X, the angle of elevation of the top is 45°. Calculate the height of the tower.
The angles of elevation of the top of a tower from two points at distance of 5 metres and 20 metres from the base of the tower and is the same straight line with it, are complementary. Find the height of the tower.
The shadow of a tower at a time is three times as long as its shadow when the angle of elevation of the sun is 60°. Find the angle of elevation of the sun at the time of the longer shadow ?
From the top of a tower of height 50 m, the angles of depression of the top and bottom of a pole are 30° and 45° respectively. Find
(i) how far the pole is from the bottom of a tower,
(ii) the height of the pole. (Use \[\sqrt{3} = 1 . 732\])
A bucket is in the form of a frustum of a cone and it can hold 28.49 litres of water. If the radii of its circular ends are 28 cm and 21 cm, find the height of the bucket. [Use`pi22/7` ]
The angles of elevation and depression of the top and bottom of a light-house from the top of a 60 m high building are 30° and 60° respectively. Find (i) the difference between the heights of the light-house and the building. (ii) the distance between the light-house and the building.
The ratio of the length of a rod and its shadow is `1 : sqrt3`. The angle of elevation of the sum is
The angle of elevation of the top of a cell phone tower from the foot of a high apartment is 60° and the angle of depression of the foot of the tower from the top of the apartment is 30°. If the height of the apartment is 50 m, find the height of the cell phone tower. According to radiation control norms, the minimum height of a cell phone tower should be 120 m. State if the height of the above mentioned cell phone tower meets the radiation norms
From a point on a bridge across a river, the angles of depression of the banks on opposite sides of the river are 30° and 45°. If the bridge is at a height of 8 m from the banks, then find the width of the river.