Advertisements
Advertisements
प्रश्न
The angle of elevation of the top of a tower from certain point is 30°. If the observer moves 20 metres towards the tower, the angle of elevation of the top increases by 15°. Find the height of the tower.
उत्तर
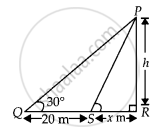
Let the height of the tower be h.
Also, SR = x m,
Given that, QS = 20 m
`sqrt("PQR")` = 30°
And `sqrt("PSR") = sqrt("PQR") + 15^circ`
= 30° + 15°
= 45°
Now, In ∆PSR,
tan 45° = `"PR"/"SR" = "h"/x`
⇒ `1 = "h"/x` ...[∵ tan 45° = 1]
⇒ x = h ...(i)
Now, In ∆PQR
tan 30° = `"PR"/"QR" = "PR"/("QS" + "SR")`
⇒ tan 30° = `"h"/(20 + x)`
⇒ 20 + x = `"h"/(tan 30^circ) = "h"/(1/sqrt(3))`
⇒ 20 + x = `"h"sqrt(3)`
⇒ 20 + h = `"h"sqrt(3)` ...[From (i)]
⇒ 20 = `"h"sqrt(3) - "h"`
⇒ `"h"(sqrt(3) - 1)` = 20
⇒ h = `20/(sqrt(3) - 1) * (sqrt(3) + 1)/(sqrt(3) + 1)` ...[By rationalisation]
⇒ h = `(20(sqrt(3) + 1))/(3 - 1) = (20(sqrt(3) + 1))/2`
⇒ h = `10(sqrt(3) + 1) "m"`
Hence, the required height of tower is `10(sqrt(3) + 1) "m"`.
APPEARS IN
संबंधित प्रश्न
The angle of elevation of a cliff from a fixed point is θ. After going up a distance of k metres towards the top of cliff at an angle of φ, it is found that the angle of elevation is α. Show that the height of the cliff is metres
On a horizontal plane, there is a vertical tower with a flagpole on the top of the tower. At a point 9 meters away from the foot of the tower the angle of elevation of the top and bottom of the flagpole are 60° and 30° respectively. Find the height of the tower and the flagpole mounted on it.
From the point of a tower 100m high, a man observe two cars on the opposite sides to the tower with angles of depression 30° and 45 respectively. Find the distance between the cars
What is the angle of elevation of the Sun when the length of the shadow of a vetical pole is equal to its height?
A man in a boat rowing away from a lighthouse 100 m high takes 2 minutes to change the angle of elevation of the top of the lighthouse from 60° to 30°.
Find the speed of the boat in metres per minute. [Use `sqrt(3` = 1.732]Use 3=1.732">
Two ships are sailing in the sea on either side of the lighthouse. The angles of depression of two ships as observed from the top of the lighthouse are 60° and 45° respectively. If the distance between the ships is `200[(sqrt(3) + 1)/sqrt(3)]` metres, find the height of the lighthouse.
At some time of the day, the length of the shadow of a tower is equal to its height. Then, the sun’s altitude at that time is ______.
A contractor plans to install two slides for the children to play in a park. For the children below the age of 5 years, she prefers to have a slide whose top is at a height of 2m and is inclined at an angle of 30° to the ground. What should be the length of the slide?
A ladder 15 metres long just reaches the top of a vertical wall. If the ladder makes an angle of 60° with the wall, find the height of the wall.
From the base of a pole of height 20 meter, the angle of elevation of the top of a tower is 60°. The pole subtends an angle 30° at the top of tower. Then the height of tower is ______.
