Advertisements
Advertisements
प्रश्न
What is the angle of elevation of the Sun when the length of the shadow of a vetical pole is equal to its height?
उत्तर
Let C be the angle of elevation of sun is θ.
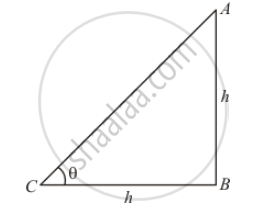
Given that: Height of pole is h meters and length of shadow is h meters. Because length of shadow is equal to the height of pole.
Here we have to find angle of elevation of sun.
So we use trigonometric ratios.
In a triangle ABC,
`⇒ tan θ=(AB)/(BC)`
`⇒ tan θ = h/h`
`⇒ tan θ=1`
`⇒θ=45°`
Hence the angle of elevation of sun is `45°`
APPEARS IN
संबंधित प्रश्न
A boat is being rowed away from a cliff 150m high. At the top of the cliff the angle of depression of the boat changes from 60º to 45º in 2 minutes. Find the speed of the boat.
A vertical tower stands on a horizontal plane and is surmounted by a vertical flag-staff of height 5 meters. At a point on the plane, the angles of elevation of the bottom and the top of the flag-staff are respectively 300 and 600. Find the height of the tower.
An observer 1.5m tall is 30 away from a chimney. The angle of elevation of the top of the chimney from his eye is 60 . Find the height of the chimney.
The angle of elevation of an aeroplane from a point on the ground is 45° after flying for 15seconds, the elevation changes to 30° . If the aeroplane is flying at a height of 2500 meters, find the speed of the areoplane.
From the top of a light house, the angles of depression of two ships on the opposite sides of it are observed to be α and β. If the height of the light house be h metres and the line joining the ships passes through the foot of the light house, show that the distance between the ship is
`(h (tan ∝+tan ß))/ (tan ∝+tan ∝)`
If the angles of elevation of the top of a tower from two points distant a and b from the base and in the same straight line with it are complementary, then the height of the tower is
The tops of two poles of height 16 m and 10 m are connected by a wire of length lmetres. If the wire makes an angle of 30° with the horizontal, then l =
The height of the vertical pole is \[\sqrt{3}\] times the length of its shadow on the ground, then angle of elevation of the sun at that time is
The tops of two poles of heights 20 m and 14 m are connected by a wire. If the wire makes an angle of 30° with the horizontal, then the length of the wire is ____________.
As observed from the top of a light house 100 m above sea level, the angle of depression of a ship, sailing directly towards it, changes from 30° to 45°. Determine the distance travelled by the ship during this time. [Use `sqrt(3)` = 1.732]

