Advertisements
Advertisements
प्रश्न
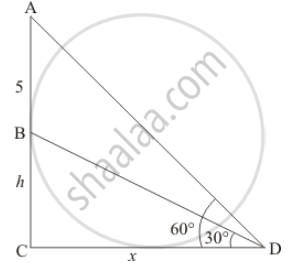
A vertical tower stands on a horizontal plane and is surmounted by a vertical flag-staff of height 5 meters. At a point on the plane, the angles of elevation of the bottom and the top of the flag-staff are respectively 300 and 600. Find the height of the tower.
उत्तर
Let BC be the tower of height, hm and AB be the Flagstaff with distance 5m. Then the angle of elevation from the top and bottom of Flagstaff are 60° and 30° respectively.
Let `CD= x` and `∠ADC = 60^@` ∠BDC = 30°
Here we have to find height h of tower.
So we use trigonometric ratios.
In a triangle BCD
`=> tan D = (BC)/(CD)`
`=> tan 30^@ = h/x`
`=> 1/sqrt3 = h/x`
`=> x = sqrt3h`
Again in a triangle ACD
`=> tan D = (AB + BC)/(CD)`
`=> tan 60^@ = (h + 5)/x`
`=> sqrt3 = (h + 5)/x`
`=> sqrt3x = h + 5`
`=> sqrt3 xx hsqrt3 = h + 5`
`=> 3h = h + 5`
`=> 2h = 5`
=> h = 2.5
Hence the height of tree is 2.5 m
APPEARS IN
संबंधित प्रश्न
A bus travels at a certain average speed for a distance of 75 km and then travels a distance of 90 km at an average speed of 10 km/h more than the first speed. If it takes 3 hours to complete the total journey, find its first speed?
The shadow of a building is 20 m long when the angle of elevation of the sun is 60º. Find the height of the building
From the top of a 50 m high tower, the angles of depression of the top and bottom of a pole are observed to be 45° and 60° respectively. Find the height of the pole.
The angle of depression of a car parked on the road from the top of a 150 m high tower is 30º. The distance of the car from the tower (in metres) is
A ladder makes an angle of 60º with the ground when placed against a wall. If the foot of the ladder is 2 m away from the wall, then the length of the ladder (in metres) is
A TV tower stands vertically on a bank of a canal, with a height of `10 sqrt3` m. From a point on the other bank directly opposite the tower, the angle of elevation of the top of the tower is 60°. From another point on the line joining this point to the foot of the tower, the angle of elevation of the top of the tower is 30°. Find the distance between the opposite bank of the canal and the point with a 30° angle of elevation.
A ladder 15 metres long just reaches the top of a vertical wall. If the ladder makes an angle of 60° with the wall, find the height of the wall.
From the top of building AB, a point C is observed on the ground whose angle of depression is 60° and which is at a distance of 40 m from the base of the building. Complete the following activity to find the height of building AB.

From figure, BC = `square`, ∠ACB = `square`
In ΔACB,
tan `square = square/(BC)`
⇒ `square = square/square`
⇒ `square = square`
Hence, the height of the building AB is `square`.
Lakshaman Jhula is located 5 kilometers north-east of the city of Rishikesh in the Indian state of Uttarakhand. The bridge connects the villages of Tapovan to Jonk. Tapovan is in Tehri Garhwal district, on the west bank of the river, while Jonk is in Pauri Garhwal district, on the east bank. Lakshman Jhula is a pedestrian bridge also used by motorbikes. It is a landmark of Rishikesh. A group of Class X students visited Rishikesh in Uttarakhand on a trip. They observed from a point (P) on a river bridge that the angles of depression of opposite banks of the river are 60° and 30° respectively. The height of the bridge is about 18 meters from the river. |
Based on the above information answer the following questions.
- Find the distance PA.
- Find the distance PB
- Find the width AB of the river.
[OR]
Find the height BQ if the angle of the elevation from P to Q be 30°.
If the height of the tower is equal to the length of its shadow, then the angle of elevation of the sun is ______.
