Advertisements
Advertisements
प्रश्न
The angle of depression of a car parked on the road from the top of a 150 m high tower is 30º. The distance of the car from the tower (in metres) is
पर्याय
\[50\sqrt{3}\]
\[150\sqrt{3}\]
\[150\sqrt{2}\]
75
उत्तर
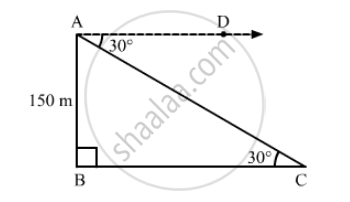
Suppose AB is the tower and C is the position of the car from the base of the tower.
It is given that, AB = 150 m
Now,
\[\angle\]ACB =\[\angle\]CAD = 30° (Alternate angles)
In right ∆ABC,
\[\tan30°= \frac{AB}{BC}\]
\[ \Rightarrow \frac{1}{\sqrt{3}} = \frac{150}{BC}\]
\[ \Rightarrow BC = 150\sqrt{3} m\]
Thus, the distance of the car from the tower is 150\[\sqrt{3}\] m.
APPEARS IN
संबंधित प्रश्न
A man standing on the deck of a ship, which is 10 m above water level, observes the angle of elevation of the top of a hill as 60° and the angle of depression of the base of a hill as 30°. Find the distance of the hill from the ship and the height of the hill
The angle of elevation of the top Q of a vertical tower PQ from a point X on the ground is 60°. From a point Y, 40 m vertically above X, the angle of elevation of the top Q of tower is 45. Find the height of the tower PQ and the distance PX. (Use `sqrt3=1.73)`
The altitude of the sun at any instant is 60º. Find the height of the vertical pole that will cast a shadow of 30 m.
From a point on the ground 40 m away from the foot of a tower, the angle of elevation of the top of the tower is 30º. The angle of elevation of the top of a water tank (on the top of the tower) is 45º. Find the (i) height of the tower (ii) the depth of the tank.
From a point P on the ground the angle of elevation of a 10 m tall building is 30°. A flag is hoisted at the top of the building and the angle of elevation of the top of the flag-staff from P is 45°. Find the length of the flag-staff and the distance of the building from the point P. (Take `sqrt3` = 1.732)
The angles of depression of the top and bottom of a tower as seen from the top of a 60 `sqrt(3)` m high cliff are 45° and 60° respectively. Find the height of the tower.
Find the positive value of m for which the distance between the points A(5, −3) and B(13, m) is 10 units.
A flag pole ‘h’ metres is on the top of the hemispherical dome of radius ‘r’ metres. A man is standing 7 m away from the dome. Seeing the top of the pole at an angle 45° and moving 5 m away from the dome and seeing the bottom of the pole at an angle 30°. Find radius of the dome `(sqrt(3) = 1.732)`
Two persons are standing ‘x’ metres apart from each other and the height of the first person is double that of the other. If from the middle point of the line joining their feet an observer finds the angular elevations of their tops to be complementary, then the height of the shorter person (in metres) is
A 1.5 m tall boy is standing at some distance from a 31.5 m tall building. If he walks ’d’ m towards the building the angle of elevation of the top of the building changes from 30° to 60°. Find the length d. (Take `sqrt3 = 1.73`)
