Advertisements
Advertisements
प्रश्न
A vertical tower stands on a horizontal plane and is surmounted by a vertical flag-staff of height 5 meters. At a point on the plane, the angles of elevation of the bottom and the top of the flag-staff are respectively 300 and 600. Find the height of the tower.
उत्तर
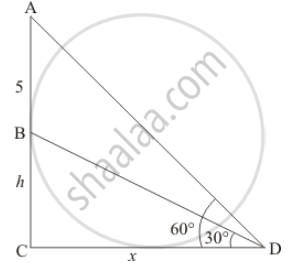
Let BC be the tower of height, hm and AB be the Flagstaff with distance 5m. Then the angle of elevation from the top and bottom of Flagstaff are 60° and 30° respectively.
Let `CD= x` and `∠ADC = 60^@` ∠BDC = 30°
Here we have to find height h of tower.
So we use trigonometric ratios.
In a triangle BCD
`=> tan D = (BC)/(CD)`
`=> tan 30^@ = h/x`
`=> 1/sqrt3 = h/x`
`=> x = sqrt3h`
Again in a triangle ACD
`=> tan D = (AB + BC)/(CD)`
`=> tan 60^@ = (h + 5)/x`
`=> sqrt3 = (h + 5)/x`
`=> sqrt3x = h + 5`
`=> sqrt3 xx hsqrt3 = h + 5`
`=> 3h = h + 5`
`=> 2h = 5`
=> h = 2.5
Hence the height of tree is 2.5 m
APPEARS IN
संबंधित प्रश्न
The angle of elevation of the top Q of a vertical tower PQ from a point X on the ground is 60°. From a point Y, 40 m vertically above X, the angle of elevation of the top Q of tower is 45. Find the height of the tower PQ and the distance PX. (Use `sqrt3=1.73)`
The angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m from the base of the tower and in the same straight line with it are 60° and 30° respectively. Find the height of the tower.
A man on a cliff observes a fishing trawler at an angle of depression of 30º which is approaching the shore to the point immediately beneath the observer with a uniform speed. 6 minutes later, the angle of depression of the trawler is found to be 60º. Caliculate the time taken by the trawler to reach the shore
From a point on the ground 40 m away from the foot of a tower, the angle of elevation of the top of the tower is 30º. The angle of elevation of the top of a water tank (on the top of the tower) is 45º. Find the (i) height of the tower (ii) the depth of the tank.
The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 50 m high, find the height of the building.
On a horizonal plane there is a vertical tower with a flagpole on the top of the tower. At a point, 9 meters away from the foot of the tower, the angle of elevation of the top and bottom of the flagpole are 60 and 30 respectively. Find the height of the tower and the flagpole mounted on it.
If the angles of elevation of the top of a tower from two points distant a and b from the base and in the same straight line with it are complementary, then the height of the tower is
A pole of height 30 m is observed from a point. The angle of depression of the point is 30°. Find the distance of the point from the base of the pole.
From a point on a bridge across a river, the angles of depression of the banks on opposite sides of the river are 30° and 45°. If the bridge is at a height of 8 m from the banks, then find the width of the river.
The top of a hill when observed from the top and bottom of a building of height h is at angles of elevation p and q respectively. What is the height of the hill?
