Advertisements
Advertisements
Question
A vertical tower stands on a horizontal plane and is surmounted by a vertical flag-staff of height 5 meters. At a point on the plane, the angles of elevation of the bottom and the top of the flag-staff are respectively 300 and 600. Find the height of the tower.
Solution
Let BC be the tower of height, hm and AB be the Flagstaff with distance 5m. Then the angle of elevation from the top and bottom of Flagstaff are 60° and 30° respectively.
Let `CD= x` and `∠ADC = 60^@` ∠BDC = 30°
Here we have to find height h of tower.
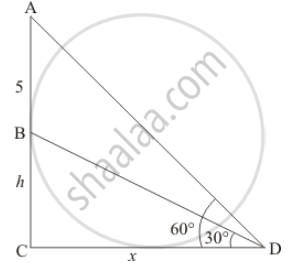
So we use trigonometric ratios.
In a triangle BCD
`=> tan D = (BC)/(CD)`
`=> tan 30^@ = h/x`
`=> 1/sqrt3 = h/x`
`=> x = sqrt3h`
Again in a triangle ACD
`=> tan D = (AB + BC)/(CD)`
`=> tan 60^@ = (h + 5)/x`
`=> sqrt3 = (h + 5)/x`
`=> sqrt3x = h + 5`
`=> sqrt3 xx hsqrt3 = h + 5`
`=> 3h = h + 5`
`=> 2h = 5`
=> h = 2.5
Hence the height of tree is 2.5 m
APPEARS IN
RELATED QUESTIONS
From the top of a building 30 m high, the top and bottom of a tower are observed to have angles of depression 30º and 45º respectively. Find the height of the tower
A man observes a car from the top of a tower, which is moving towards the tower with a uniform speed. If the angle of depression of the car changes from 30° to 45° in 12 minutes, find the time taken by the car now to reach the tower.
A kit is flying at a height of 75 metres from the ground level, attached to a string inclined at 60 to the horizontal. Find the length of the string to the nearest metre.
A man on the deck of a ship is 10 m above the water level. He observes that the angle of elevation of the top of a cliff is 45° and the angle of depression of the base is 300. Calculate the distance of the cliff from the ship and the height of the cliff.
Two men are on opposite side of tower. They measure the angles of elevation of the top of the tower as 30 and 45 respectively. If the height of the tower is 50 meters, find the distance between the two men.
The horizontal distance between two poles is 15 m. The angle of depression of the top of first pole as seen from the top of second pole is 30°. If the height of the second pole is 24 m, find the height of the first pole. Use`[sqrt3=1.732]`
The angle of elevation of a cloud from a point h metre above a lake is θ. The angle of depression of its reflection in the lake is 45°. The height of the cloud is
The angle of elevation of the top of a tower at a point on the ground 50 m away from the foot of the tower is 45º. Then the height of the tower (in metres) is
A ladder 15 metres long just reaches the top of a vertical wall. If the ladder makes an angle of 60° with the wall, find the height of the wall.
If the height of the tower is equal to the length of its shadow, then the angle of elevation of the sun is ______.
