Advertisements
Advertisements
Question
The horizontal distance between two poles is 15 m. The angle of depression of the top of first pole as seen from the top of second pole is 30°. If the height of the second pole is 24 m, find the height of the first pole. Use`[sqrt3=1.732]`
Solution
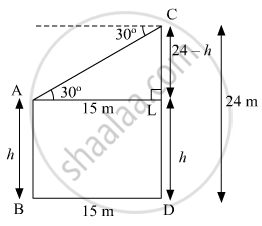
Let AB and CD be two poles, where CD = 24 m.
It is given that angle of depression of the top of the pole AB as seen from the top of the pole CD is 30° and horizontal distance between the two poles is 15 m.
∴ ∠CAL = 30° and BD = 15 m.
To find: Height of pole AB
Let the height of pole AB be h m.
AL = BD = 15 m and AB = LD = h
Therefore, CL = CD − LD = 24 − h
Consider right ΔACL:
`tan angleCAL =\text{perpendicular}/\text{Base}=(CL)/(AL)`
`rArrtan 30^o=(24-h)/15`
`rArr 24-h=15/sqrt3`
`rArr24-h=5sqrt3`
`rArrh=24-5sqrt3`
`rArrh=24-5xx1.732` `[\text{Taking}sqrt3=1.732]`
`rArrh=15.34`
Therefore, height of the pole AB = h m = 15.34 m.
APPEARS IN
RELATED QUESTIONS
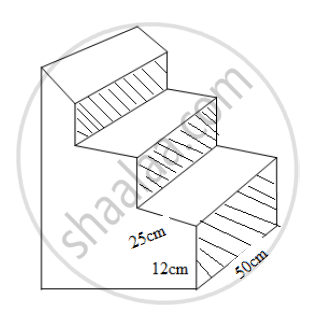
There are three stair-steps as shown in the figure below. Each stair step has width 25 cm, height 12 cm and length 50 cm. How many bricks have been used in it, if each brick is 12.5 cm x 6.25 cm x 4 cm?
The vertical tower stands on a horizontal plane and is surmounted by a vertical flagstaff of height 6m. At a point on the plane, the angle of elevation of the bottom of the flagstaff is
30 and that of the top of the flagstaff 60 . Find the height of the tower
[Use `sqrt(3)` 1.732 ]
The angle of elevation of the top Q of a vertical tower PQ from a point X on the ground is 60° . At a point Y, 40m vertically above X, the angle of elevation is 45° . Find the height of tower PQ.
If the angles of elevation of a tower from two points distant a and b (a>b) from its foot and in the same straight line from it are 30° and 60°, then the height of the tower is
From a light house the angles of depression of two ships on opposite sides of the light house are observed to be 30° and 45°. If the height of the light house is h metres, the distance between the ships is
The angle of elevation of the top of a tower at a point on the ground 50 m away from the foot of the tower is 45º. Then the height of the tower (in metres) is
The horizontal distance between two buildings is 70 m. The angle of depression of the top of the first building when seen from the top of the second building is 45°. If the height of the second building is 120 m, find the height of the first building
The electric pole subtends an angle of 30° at a point on the same level as its foot. At a second point ‘b’ metres above the first, the depression of the foot of the pole is 60°. The height of the pole (in metres) is equal to
A vertical tower stands on a horizontal plane and is surmounted by a vertical flag staff of height h. At a point on the plane, the angles of elevation of the bottom and the top of the flag staff are α and β, respectively. Prove that the height of the tower is `((h tan α)/(tan β - tan α))`.
From the top of a 7 m high building, the angle of elevation of the top of a cable tower is 60° and the angle of depression of its foot is 30°. Determine the height of the tower.
