Advertisements
Advertisements
Question
The horizontal distance between two buildings is 70 m. The angle of depression of the top of the first building when seen from the top of the second building is 45°. If the height of the second building is 120 m, find the height of the first building
Solution
Let the height of the first building AD be x m
∴ EC = 120 – x
In the right ∆CDE,
tan 45° = `"CE"/"CD"`
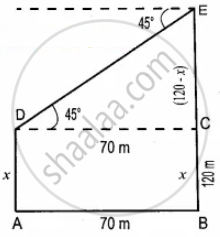
1 = `(120 - x)/70`
⇒ 70 = 120 – x
x = 50 cm
∴ The height of the first building is 50 m
APPEARS IN
RELATED QUESTIONS
As observed from the top of a 75 m high lighthouse from the sea-level, the angles of depression of two ships are 30° and 45°. If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships.
Two points A and B are on the same side of a tower and in the same straight line with its base. The angles of depression of these points from the top of the tower are 60° and 45° respectively. If the height of the tower is 15 m, then find the distance between the points.
The angle of elevation of the top of a tower from a point A on the ground is 30°. Moving a distance of 20metres towards the foot of the tower to a point B the angle of elevation increases to 60°. Find the height of the tower & the distance of the tower from the point A.
Two buildings are in front of each other on a road of width 15 meters. From the top of the first building, having a height of 12 meter, the angle of elevation of the top of the second building is 30°.What is the height of the second building?
What is the angle of elevation of the Sun when the length of the shadow of a vetical pole is equal to its height?
The angle of depression of a car, standing on the ground, from the top of a 75 m tower, is 30°. The distance of the car from the base of the tower (in metres) is
In figure given ABCD is a rectangle, the value of CE is ____________.

An observer 1.5 m tall is 28.5 m away from a tower. The angle of elevation of the top of the tower from her eyes is 45°. What is the height of the tower?
Read the following passage and answer the questions given below.
|
Qutub Minar, located in South Delhi, India was built in the year 1193. It is 72 m high tower. Working on a school project, Charu and Daljeet visited the monument. They used trigonometry to find their distance from the tower. Observe the picture given below. Points C and D represent their positions on the ground in line with the base of tower, the angles of elevation of top of the tower (Point A) are 60° and 45° from points C and D respectively.
|
- Based on the above information, draw a well-labelled diagram.
- Find the distances CD, BC and BD. [use `sqrt(3)` = 1.73]
Two pillars of equal lengths stand on either side of a road which is 100 m wide, exactly opposite to each other. At a point on the road between the pillars, the angles of elevation of the tops of the pillars are 60° and 30°. Find the length of each pillar and the distance of the point on the road from the pillars. (Use `sqrt3` = 1.732)

