Advertisements
Advertisements
Question
The angle of elevation of the top of a tower from a point A on the ground is 30°. Moving a distance of 20metres towards the foot of the tower to a point B the angle of elevation increases to 60°. Find the height of the tower & the distance of the tower from the point A.
Solution
Let h be the height of the tower and the angle of elevation of the top of the tower from a point A on the ground is 30° and on moving with distance 20 m towards the foot of tower on the point B is 60°.
Let AB = 20 and BC = x
Now we have to find the height of tower and distance of tower from point A.
So we use trigonometrical ratios.
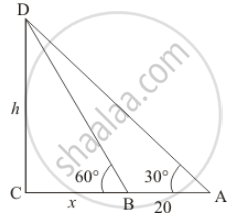
In ΔDBC
`=> tan D = (CD)/(BC)`
`=> tan 60^@ = (CD)/(BC)
`=> sqrt3 = h/x`
`=> x = h/sqrt3`
Again in Δ DAC
`=> tan A = (CD)/(BC + BA)`
`=> tan 30^@ = h/(x + 20)`
`=> 1/sqrt3 = h/(x + 20)`
`=> x = sqrt3h - 20`
`=> h/sqrt3 + 20 = sqrt3h`
`=> h/sqrt3 - sqrt3h = -20`
`=> h - 3h = -20sqrt3`
`=> -2h = -20sqrt3`
`=> h = 10sqrt3`
`=> h = 17.32`
`=> x = (10sqrt3)/sqrt3`
`=> x = 10`
So distance
`=> AC = x + 20`
=> AC = 30
Hence the required height is 17.32 m and distance is 30 m
APPEARS IN
RELATED QUESTIONS
At the foot of a mountain the elevation of its summit is 45º; after ascending 1000 m towards the mountain up a slope of 30º inclination is found to be 60º. Find the height of the mountain.
The shadow of a tower, when the angle of elevation of the sun is 45°, is found to be 10 m. longer than when it was 600. Find the height of the tower.
Two boats approach a lighthouse in mid-sea from opposite directions. The angles of elevation of the top of the lighthouse from two boats are 30° and 45° respectively. If the distance between two boats is 100 m, find the height of the lighthouse.
The horizontal distance between two towers is 60 meters. The angle of depression of the top of the first tower when seen from the top of the second tower is 30° . If the height of the second tower is 90 meters. Find the height of the first tower.
The angle of elevation of an aeroplane from a point on the ground is 45° after flying for 15seconds, the elevation changes to 30° . If the aeroplane is flying at a height of 2500 meters, find the speed of the areoplane.
Two ships are approaching a light-house from opposite directions. The angles of depression of the two ships from the top of the light-house are 30° and 45°. If the distance between the two ships is 100 m, find the height of the light-house. \[[Use \sqrt{3} = 1 . 732]\]
The height of a tower is 100 m. When the angle of elevation of the sun changes from 30° to 45°, the shadow of the tower becomes x metres less. The value of x is
Two ships are sailing in the sea on either side of the lighthouse. The angles of depression of two ships as observed from the top of the lighthouse are 60° and 45° respectively. If the distance between the ships is `200[(sqrt(3) + 1)/sqrt(3)]` metres, find the height of the lighthouse.
The angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of the tower is 30°. The length of the tower is ____________.
A TV tower stands vertically on a bank of a canal, with a height of `10 sqrt3` m. From a point on the other bank directly opposite the tower, the angle of elevation of the top of the tower is 60°. From another point on the line joining this point to the foot of the tower, the angle of elevation of the top of the tower is 30°. Find the distance between the opposite bank of the canal and the point with a 30° angle of elevation.
