Advertisements
Advertisements
Question
Two boats approach a lighthouse in mid-sea from opposite directions. The angles of elevation of the top of the lighthouse from two boats are 30° and 45° respectively. If the distance between two boats is 100 m, find the height of the lighthouse.
Solution
Let h be the height of lighthouse BD. An angle of elevation of the top of the lighthouse from two boats is 30° and 45°.
Let DB = h , BC = x and it is given that AC = 100 m. So
AB = 100 - x. And ∠DAB = 30°, ∠BCD = 45°
Here we have to find height of light house.
The corresponding figure is as follows
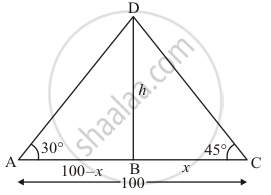
So we use trigonometric ratios.
In ΔBDC
`=> tan 45° = (BD)/(BC)`
`=> 1 = h/x`
`=> x = h `
Again in ΔDAB
`=> tan 30° = (DB)/(AB)`
`=> 1/sqrt3 = h/(100 - x)`
`=> sqrt3h = 100 - x`
`=> (sqrt3 + 1)h = 100`
`=> h = 100/(sqrt3 + 1) xx (sqrt3 - 1)/(sqrt3 - 1)`
`=> h = 50(sqrt3 - 1)`
Hence the height of light house is `50(sqrt3 - 1)` m
APPEARS IN
RELATED QUESTIONS
If the angle of elevation of cloud from a point 200 m above a lake is 30º and the angle of depression of its reflection in the lake is 60º, then find the height of the cloud above the lake
A tree breaks due to storm and the broken part bends so that the top of the tree touches the ground, making an angle 30° with it. The distance between the foot of the tree to the point where the top touches the ground is 8 m. Find the height of the tree.
The shadow of a tower at a time is three times as long as its shadow when the angle of elevation of the sun is 60°. Find the angle of elevation of the sun at the time of the longer shadow ?
The length of shadow of a tower on the plane ground is `sqrt3` times the height of the tower.
The angle of elevation of sun is:
Water flows at the rate of 10 meters per minute through a cylindrical pipe having its diameter 20 mm. how much time will it take to fill a conical vessel of diameter 40 cm and depth 24 cm?
A man in a boat rowing away from a lighthouse 100 m high takes 2 minutes to change the angle of elevation of the top of the lighthouse from 60° to 30°.
Find the speed of the boat in metres per minute. [Use `sqrt(3` = 1.732]Use 3=1.732">
From the top of a lighthouse, the angle of depression of two ships on the opposite sides of it is observed to be 30° and 60°. If the height of the lighthouse is h meters and the line joining the ships passes through the foot of the lighthouse, show that the distance between the ships is `(4"h")/sqrt(3)` m
In figure given ABCD is a rectangle, the value of CE is ____________.

If the length of the shadow of a tower is increasing, then the angle of elevation of the sun is also increasing.
A boy 1.7 m tall is standing on a horizontal ground, 50 m away from a building. The angle of elevation of the top of the building from his eye is 60°. Calculate the height of the building. (Take `sqrt(3)` = 1.73)
