Advertisements
Advertisements
Question
A man in a boat rowing away from a lighthouse 100 m high takes 2 minutes to change the angle of elevation of the top of the lighthouse from 60° to 30°.
Find the speed of the boat in metres per minute. [Use `sqrt(3` = 1.732]Use 3=1.732">
Solution
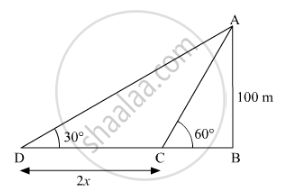
AB is a lighthouse of height 100m.
Let the speed of the boat be x metres per minute.
And CD is the distance which man travelled to change the angle of elevation.
So, CD = 2x ...[∵ Distance = Speed x Time]
tan (60°) = `("AB")/("BC")`
`sqrt(3) = (100)/("BC")`
⇒ `"BC" = (100)/(sqrt(3)`
tan (30°) = `("AB")/("BD")`
`(1)/sqrt(3) = (100)/("BD")`
`"BD" = 100 sqrt(3)`
`"CD"= "BD" - "BC"`
`2"x" = 100sqrt(3) - (100)/sqrt(3)`
`2"x" = (300-100)/sqrt(3)`
⇒ `"x" = (200)/(2sqrt(3)`
⇒ `"x" = (100)/(sqrt3)`
Using `sqrt(3)` = 1.73
`"x" = (100)/(1.73) ≈ 57.80`
Hence, the speed of the boat is 57.80">57.8057.80 metres per minute.
APPEARS IN
RELATED QUESTIONS
From the top of a lighthouse, the angles of depression of two ships on the opposite sides of it are observed to be a and 3. If the height of the lighthouse be h meters and the line joining the ships passes through the foot of the lighthouse, show that the distance
`(h(tan alpha + tan beta))/(tan alpha tan beta)` meters
The tops of two towers of height x and y, standing on level ground, subtend angles of 30º and 60º respectively at the centre of the line joining their feet, then find x : y.
The angles of depression of two ships from the top of a light house are 45° and 30° towards east. If the ships are 100 m apart. the height of the light house is
A lift in a building of height 90 feet with transparent glass walls is descending from the top of the building. At the top of the building, the angle of depression to a fountain in the garden is 60°. Two minutes later, the angle of depression reduces to 30°. If the fountain is `30sqrt(3)` feet from the entrance of the lift, find the speed of the lift which is descending.
A bird is sitting on the top of a 80 m high tree. From a point on the ground, the angle of elevation of the bird is 45°. The bird flies away horizontally in such away that it remained at a constant height from the ground. After 2 seconds, the angle of elevation of the bird from the same point is 30°. Determine the speed at which the bird flies `(sqrt(3) = 1.732)`
If at some time, the length of the shadow of a tower is `sqrt3` times its height, then the angle of elevation of the sun, at that time is ____________.
An observer 2.25 m tall is 42.75 m away from a chimney. The angle of elevation of the top of the chimney from her eyes is 45°. What is the height of the chimney?
A vertical tower stands on a horizontal plane and is surmounted by a vertical flagstaff of height h. At a point on the plane, the angles of elevation of the bottom and the top of the flagstaff are α and β, respectively. Then the height of the tower is ____________.
An observer 1.5 metres tall is 20.5 metres away from a tower 22 metres high. Determine the angle of elevation of the top of the tower from the eye of the observer.
The angle of elevation of the top of a vertical tower from a point on the ground is 60°. From another point 10 m vertically above the first, its angle of elevation is 45°. Find the height of the tower.
