Advertisements
Advertisements
Question
From the top of a lighthouse, the angles of depression of two ships on the opposite sides of it are observed to be a and 3. If the height of the lighthouse be h meters and the line joining the ships passes through the foot of the lighthouse, show that the distance
`(h(tan alpha + tan beta))/(tan alpha tan beta)` meters
Solution
Let h be the height of lighthouse AC. And an angle of depression of the top of the lighthouse from two ships is α and β respectively.
Let BC = x, CD = y. And ∠ABC = α, ∠ADC = β.
We have to find the distance between the ships
We have the corresponding figure as follows
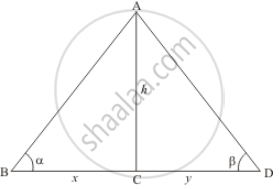
We use trigonometric ratios.
In ΔABC
`=> tan α = (AC)/(BC)`
`=> tan α = h/x`
Again in Δ ADC
`=> tan β = (AC)/(CD)`
`=> tan β = h/y`
`=> y = h/(tan β)`
Now
`=> BD = x + y`
`=> BD = h/(tan α) + h/(tan β)`
`=> BD = (h(tan α + tan β))/(tan α tan β)`
Hence the distance between ships is `(h(tan α + tan β))/(tan α tan β)`
APPEARS IN
RELATED QUESTIONS
Two ships are there in the sea on either side of a light house in such a way that the ships and the light house are in the same straight line. The angles of depression of two ships as observed from the top of the light house are 60° and 45°. If the height of the light house is 200 m, find the distance between the two ships. [use √3=1.73]
On a horizontal plane, there is a vertical tower with a flagpole on the top of the tower. At a point 9 meters away from the foot of the tower the angle of elevation of the top and bottom of the flagpole are 60° and 30° respectively. Find the height of the tower and the flagpole mounted on it.
From a point P on the ground the angle of elevation of a 10 m tall building is 30°. A flag is hoisted at the top of the building and the angle of elevation of the top of the flag-staff from P is 45°. Find the length of the flag-staff and the distance of the building from the point P. (Take `sqrt3` = 1.732)
An electrician has to repair an electric fault on a pole of height 4 meters. He needs to reach a point 1 meter below the top of the pole to undertake the repair work. What should be the length of the ladder that he should use, which when inclined at an angle of 60° to the horizontal would enable him to reach the required position?
A pole casts a shadow of length \[2\sqrt{3}\] m on the ground, when the sun's elevation is 60°. Find the height of the pole.
From the top of the light house, an observer looks at a ship and finds the angle of depression to be 30°. If the height of the light-house is 100 meters, then find how far the ship is from the light-house.
From the top of a light house, the angles of depression of two ships on the opposite sides of it are observed to be α and β. If the height of the light house be h metres and the line joining the ships passes through the foot of the light house, show that the distance between the ship is
`(h (tan ∝+tan ß))/ (tan ∝+tan ∝)`
Two poles are 25 m and 15 m high, and the line joining their tops makes an angle of 45° with the horizontal. The distance between these poles is ______.
If the length of the shadow of a tower is increasing, then the angle of elevation of the sun ____________.
As observed from the top of a light house 100 m above sea level, the angle of depression of a ship, sailing directly towards it, changes from 30° to 45°. Determine the distance travelled by the ship during this time. [Use `sqrt(3)` = 1.732]

