Advertisements
Advertisements
Question
On a horizontal plane, there is a vertical tower with a flagpole on the top of the tower. At a point 9 meters away from the foot of the tower the angle of elevation of the top and bottom of the flagpole are 60° and 30° respectively. Find the height of the tower and the flagpole mounted on it.
Solution
Let AB be the tower of height h and AD be the flagpole on the tower. At the point 9m away from the foot of the tower, the angle of elevation of the top and bottom of the flagpole is 60° and 30°
Let AD = x, BC = 9 and ∠ACB = 30°, ∠DCB = 60°
Here we have to find the height of tower and height of the flagpole.
The corresponding diagram is as follows
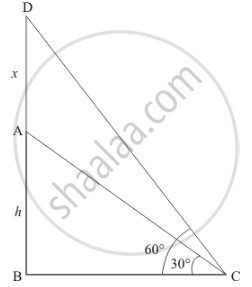
In a triangle ABC,
`=> tan C = (AB)/(BC)`
`=> tan 30^@ = h/9`
`=> 1/sqrt3 = h/9`
`=>h = 9/sqrt3`
`=> h = 3sqrt3`
Again in a triangle DBC
`=> tan C = (AD + AB)/(BC)`
`=> tan 60^@ = (h + x)/9`
`=> sqrt3 = (h + x)/9`
`=> 9sqrt3 = h + x`
`=> 9sqrt3 = 3sqrt3 + x`
`=> x = 6sqrt3`
So height of tower is `3sqrt3` meter and height of flag pole is `6sqrt3` meters
APPEARS IN
RELATED QUESTIONS
A person standing on the bank of river observes that the angle of elevation of the top of a tree standing on the opposite bank is 60°. When he moves 40 m away from the bank, he finds the angle of elevation to be 30°. Find the height of the tree and width of the river. `(sqrt 3=1.73)`
From the top of a cliff 25 m high the angle of elevation of a tower is found to be equal to the angle of depression of the foot of the tower. Find the height of the tower
A tower stands vertically on the ground. From a point on the ground, 20 m away from the foot of the tower, the angle of elevation of the top of the tower is 600. What is the height of the tower?
PQ is a post of given height a, and AB is a tower at some distance. If α and β are the angles of elevation of B, the top of the tower, at P and Q respectively. Find the height of the tower and its distance from the post.
An electrician has to repair an electric fault on a pole of height 4 meters. He needs to reach a point 1 meter below the top of the pole to undertake the repair work. What should be the length of the ladder that he should use, which when inclined at an angle of 60° to the horizontal would enable him to reach the required position?
A solid right circular cone is cut into two parts at the middle of its height by a plane parallel to its base. The ratio of the volume of the smaller cone to the whole cone is
In given figure, the length of AP is ____________.

There are two windows in a house. A window of the house is at a height of 1.5 m above the ground and the other window is 3 m vertically above the lower window. Ram and Shyam are sitting inside the two windows. At an instant, the angle of elevation of a balloon from these windows is observed as 45° and 30° respectively. Find the height of the balloon from the ground.
The angle of elevation of the top of a tower is 30°. If the height of the tower is doubled, then the angle of elevation of its top will also be doubled.
The angle of elevation of the top of a vertical tower from a point on the ground is 60°. From another point 10 m vertically above the first, its angle of elevation is 45°. Find the height of the tower.
