Advertisements
Advertisements
Question
PQ is a post of given height a, and AB is a tower at some distance. If α and β are the angles of elevation of B, the top of the tower, at P and Q respectively. Find the height of the tower and its distance from the post.
Solution
Let AB be the tower of height H and PQ is a given post of height a, α and β are angles of elevation of the top of tower AB from P and Q. Let PA = x. PQ = a and BC = h.
The corresponding figure is as follows
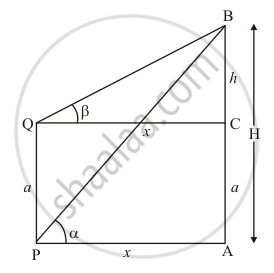
In ΔQCB
`=> tan beta = h/x`
`=> x = h/(tan beta)
Again in ΔPAB
`=> tan alpha = (h + a)/x`
`=> tan alpha = ((h + a)tan beta)/h`
`=> h tan alpha = (h + a)tan beta`
`=> h(tan alpha - tan beta) = a tan beta`
`=> h =(a tan beta)/(tan alpha - tan beta)`
Now
`=> x = (a tan beta)/((tan alpha - tan beta) xx tan beta)`
`=> x = a/(tan alpha - tan beta)`
`=> H = (a tan alpha)/(tan a - tan beta)`
Hence required heigtht is `(a tan alpha)/(tan alpha - tan beta)` And distance is `a/(tan alpha - tan beta)`
APPEARS IN
RELATED QUESTIONS
The banks of a river are parallel. A swimmer starts from a point on one of the banks and swims in a straight line inclined to the bank at 45º and reaches the opposite bank at a point 20 m from the point opposite to the starting point. Find the breadth of the river
The angle of elevation of the top of a tower from a point A due south of the tower is α and from B due east of the tower is β. If AB = d, show that the height of the tower is
`\frac{d}{\sqrt{\cot ^{2}\alpha +\cot^{2}\beta `
On the same side of a tower, two objects are located. When observed from the top of the tower, their angles of depression are 45° and 60°. If the height of the tower is 150 m, find the distance between the objects.
If the angles of elevation of a tower from two points distant a and b (a>b) from its foot and in the same straight line from it are 30° and 60°, then the height of the tower is
Two persons are a metres apart and the height of one is double that of the other. If from the middle point of the line joining their feet, an observer finds the angular elevation of their tops to be complementary, then the height of the shorter post is
The electric pole subtends an angle of 30° at a point on the same level as its foot. At a second point ‘b’ metres above the first, the depression of the foot of the pole is 60°. The height of the pole (in metres) is equal to
A TV tower stands vertically on a bank of a canal, with a height of `10 sqrt3` m. From a point on the other bank directly opposite the tower, the angle of elevation of the top of the tower is 60°. From another point on the line joining this point to the foot of the tower, the angle of elevation of the top of the tower is 30°. Find the distance between the opposite bank of the canal and the point with a 30° angle of elevation.
Read the following passage and answer the questions given below.
|
Kite Festival Kite festival is celebrated in many countries at different times of the year. In India, every year 14th January is celebrated as International Kite Day. On this day many people visit India and participate in the festival by flying various kinds of kites. The picture given below, show three kites flying together.
In the given figure, the angles of elevation of two kites (Points A and B) from the hands of a man (Point C) are found to be 30° and 60° respectively. Taking AD = 50 m and BE = 60 m, find. |
- the lengths of strings used (take them straight) for kites A and B as shown in the figure.
- the distance 'd' between these two kites.
An aeroplane at an altitude of 200 metres observes the angles of depression of opposite points on the two banks of a river to be 45° and 60°. Find the width of the river. (Use = `sqrt(3)` = 1.732)
The angle of elevation of the top P of a vertical tower PQ of height 10 from a point A on the horizontal ground is 45°. Let R be a point on AQ and from a point B, vertically above R, the angle of elevation of P is 60°. If ∠BAQ = 30°, AB = d and the area of the trapezium PQRB is α, then the ordered pair (d, α) is ______.


