Advertisements
Advertisements
Question
Read the following passage and answer the questions given below.
|
Kite Festival Kite festival is celebrated in many countries at different times of the year. In India, every year 14th January is celebrated as International Kite Day. On this day many people visit India and participate in the festival by flying various kinds of kites. The picture given below, show three kites flying together.
In the given figure, the angles of elevation of two kites (Points A and B) from the hands of a man (Point C) are found to be 30° and 60° respectively. Taking AD = 50 m and BE = 60 m, find. |
- the lengths of strings used (take them straight) for kites A and B as shown in the figure.
- the distance 'd' between these two kites.
Solution
We have the following figure
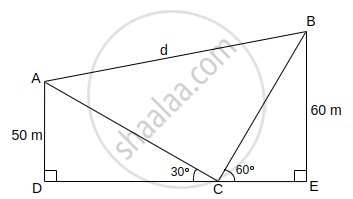
1. Clearly, In ΔADC,
sin 30° = `("AD")/("AC")`
⇒ `1/2 = 50/("AC")`
⇒ AC = 100 m
and In ΔBEC,
sin 60° = `("BE")/("BC")`
⇒ `sqrt(3)/2 = 60/("BC")`
⇒ BC = `120/sqrt(3) = 40sqrt(3)` m
Thus, the lengths of strings used are 100 m and `40sqrt(3)` m.
2. Since, DCE is a straight line.
∴ ∠DCA + ∠ACB + ∠BCE = 180°
⇒ 30° + ∠ACB + 60° = 180°
⇒ ∠ACB = 90°
∴ ∠ACB is a right triangle.
Now applying Pythagoras theorem, in ΔABC,
(AB)2 = (AC)2 + (BC)2
⇒ (d)2 = `(100)^2 + (40sqrt(3))^2`
⇒ d2 = 10000 + 1600 × 3
⇒ d2 = 14800
⇒ d = `20sqrt(37)` m
APPEARS IN
RELATED QUESTIONS
The angle of elevation of the top Q of a vertical tower PQ from a point X on the ground is 60°. From a point Y, 40 m vertically above X, the angle of elevation of the top Q of tower is 45. Find the height of the tower PQ and the distance PX. (Use `sqrt3=1.73)`
If the angle of elevation of cloud from a point 200 m above a lake is 30º and the angle of depression of its reflection in the lake is 60º, then find the height of the cloud above the lake
Two persons are a metres apart and the height of one is double that of the other. If from the middle point of the line joining their feet, an observer finds the angular elevation of their tops to be complementary, then the height of the shorter post is
From the top of the tower 60 m high the angles of depression of the top and bottom of a vertical lamp post are observed to be 38° and 60° respectively. Find the height of the lamp post (tan 38° = 0.7813, `sqrt(3)` = 1.732)
A bird is flying from A towards B at an angle of 35°, a point 30 km away from A. At B it changes its course of flight and heads towards C on a bearing of 48° and distance 32 km away. How far is C to the East of B?
(sin 55° = 0.8192, cos 55° = 0.5736, sin 42° = 0.6691, cos 42° = 0.7431)
A circus artist is climbing a 20 m long rope, which is tightly stretched and tied from the top of a vertical pole to the ground. Find the height of the pole if the angle made by the rope with the ground level is 30°.
The angle of elevation of the top of a tower from certain point is 30°. If the observer moves 20 metres towards the tower, the angle of elevation of the top increases by 15°. Find the height of the tower.
The top of a banquet hall has an angle of elevation of 45° from the foot of a transmission tower and the angle of elevation of the topmost point of the tower from the foot of the banquet hall is 60°. If the tower is 60 m high, find the height of the banquet hall in decimals.
From a point on a bridge across a river, the angles of depression of the banks on opposite sides of the river are 30° and 45°. If the bridge is at a height of 8 m from the banks, then find the width of the river.
|
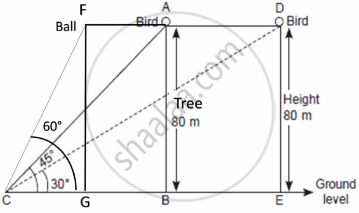
One evening, Kaushik was in a park. Children were playing cricket. Birds were singing on a nearby tree of height 80m. He observed a bird on the tree at an angle of elevation of 45°. When a sixer was hit, a ball flew through the tree frightening the bird to fly away. In 2 seconds, he observed the bird flying at the same height at an angle of elevation of 30° and the ball flying towards him at the same height at an angle of elevation of 60°.
|
- At what distance from the foot of the tree was he observing the bird sitting on the tree?
- How far did the bird fly in the mentioned time?
(or)
After hitting the tree, how far did the ball travel in the sky when Kaushik saw the ball? - What is the speed of the bird in m/min if it had flown `20(sqrt3 + 1) m`?