Advertisements
Advertisements
प्रश्न
Read the following passage and answer the questions given below.
|
Kite Festival Kite festival is celebrated in many countries at different times of the year. In India, every year 14th January is celebrated as International Kite Day. On this day many people visit India and participate in the festival by flying various kinds of kites. The picture given below, show three kites flying together.
In the given figure, the angles of elevation of two kites (Points A and B) from the hands of a man (Point C) are found to be 30° and 60° respectively. Taking AD = 50 m and BE = 60 m, find. |
- the lengths of strings used (take them straight) for kites A and B as shown in the figure.
- the distance 'd' between these two kites.
उत्तर
We have the following figure
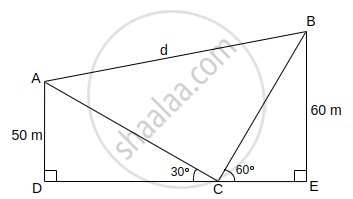
1. Clearly, In ΔADC,
sin 30° = `("AD")/("AC")`
⇒ `1/2 = 50/("AC")`
⇒ AC = 100 m
and In ΔBEC,
sin 60° = `("BE")/("BC")`
⇒ `sqrt(3)/2 = 60/("BC")`
⇒ BC = `120/sqrt(3) = 40sqrt(3)` m
Thus, the lengths of strings used are 100 m and `40sqrt(3)` m.
2. Since, DCE is a straight line.
∴ ∠DCA + ∠ACB + ∠BCE = 180°
⇒ 30° + ∠ACB + 60° = 180°
⇒ ∠ACB = 90°
∴ ∠ACB is a right triangle.
Now applying Pythagoras theorem, in ΔABC,
(AB)2 = (AC)2 + (BC)2
⇒ (d)2 = `(100)^2 + (40sqrt(3))^2`
⇒ d2 = 10000 + 1600 × 3
⇒ d2 = 14800
⇒ d = `20sqrt(37)` m
APPEARS IN
संबंधित प्रश्न
The angle of elevation of an aeroplane from a point on the ground is 60°. After a flight of 30 seconds the angle of elevation becomes 300 If the aeroplane is flying at a constant height of 3000 3 m, find the speed of the aeroplane.
The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 45°. If the tower is 30 m high, find the height of the building.
The angle of elevation of the top of a vertical tower from a point on the ground is 60° . From another point 10 m vertically above the first, its angle of elevation is 30° .Find the height of the tower.
As observed form the top of a lighthouse, 100m above sea level, the angle of depression of a ship, sailing directly towards it, changes from 30° and 60° . Determine the distance travelled by the ship during the period of observation.
A ladder 15 m long just reaches the top of a vertical wall. If the ladder makes an angle of 60° with the wall, then the height of the wall is
If the ratio of the height of a tower and the length of its shadow is `sqrt(3): 1`, then the angle of elevation of the sun has measure
Two ships are sailing in the sea on either side of the lighthouse. The angles of depression of two ships as observed from the top of the lighthouse are 60° and 45° respectively. If the distance between the ships is `200[(sqrt(3) + 1)/sqrt(3)]` metres, find the height of the lighthouse.
A 1.5 m tall boy is standing at some distance from a 31.5 m tall building. If he walks ’d’ m towards the building the angle of elevation of the top of the building changes from 30° to 60°. Find the length d. (Take `sqrt3 = 1.73`)
The angle of elevation of the top of a vertical tower from a point on the ground is 60°. From another point, 10 m vertically above the first, its angle of elevation is 45°. Find the height of the tower.
The top of a hill when observed from the top and bottom of a building of height h is at angles of elevation p and q respectively. What is the height of the hill?


