Question

Read the following passage and answer the questions given below.

Kite Festival Kite festival is celebrated in many countries at different times of the year. In India, every year 14th January is celebrated as International Kite Day. On this day many people visit India and participate in the festival by flying various kinds of kites. The picture given below, show three kites flying together. In the given figure, the angles of elevation of two kites (Points A and B) from the hands of a man (Point C) are found to be 30° and 60° respectively. Taking AD = 50 m and BE = 60 m, find.

1. the lengths of strings used (take them straight) for kites A and B as shown in the figure.
2. the distance 'd' between these two kites.

Answer 1

We have the following figure

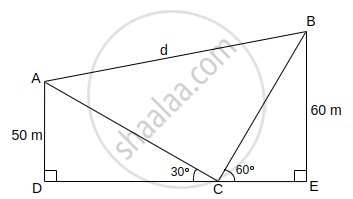
1. Clearly, In ΔADC, 

sin 30° = `("AD")/("AC")`

⇒ `1/2 = 50/("AC")`

⇒ AC = 100 m

and In ΔBEC,

sin 60° = `("BE")/("BC")`

⇒ `sqrt(3)/2 = 60/("BC")`

⇒ BC = `120/sqrt(3) = 40sqrt(3)` m

Thus, the lengths of strings used are 100 m and `40sqrt(3)` m.

2. Since, DCE is a straight line.

∴ ∠DCA + ∠ACB + ∠BCE = 180°

⇒ 30° + ∠ACB + 60° = 180°

⇒ ∠ACB = 90°

∴ ∠ACB is a right triangle.

Now applying Pythagoras theorem, in ΔABC,

(AB)² = (AC)² + (BC)²

⇒ (d)² = `(100)^2 + (40sqrt(3))^2`

⇒ d² = 10000 + 1600 × 3

⇒ d² = 14800

⇒ d = `20sqrt(37)` m