Advertisements
Advertisements
प्रश्न
A kite is flying at a height of 75 in from the level ground, attached to a string inclined at 60°. to the horizontal. Find the length of the string, assuming that there is no slack in it.
[Take `sqrt(3)` =1.732 ]
उत्तर
Let OX be the horizontal ground and A be the position of the kite.
Also, let O be the position of the observer and OA be the thread.
Now, draw AB ⊥ OX.
We have:
∠BOA= 60°,OA= 75m and ∠OBA = 90°
Height of the kite from the ground = AB = 75 m
Length of the string OA = xm
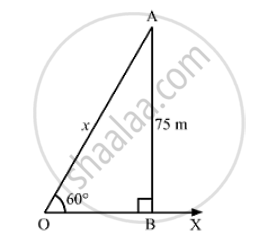
In the right ΔOBA,we have:
`(AB)/(OA ) = sin 60° = sqrt(3)/2`
`⇒ 75/x = sqrt(3)/2`
`⇒ x = (75xx2)/sqrt(3) = 150/1.732 = 86.6m`
Hence, the length of the string is 86.6m
APPEARS IN
संबंधित प्रश्न
From a point P on the ground the angle of elevation of a 10 m tall building is 30°. A flag is hoisted at the top of the building and the angle of elevation of the top of the flag-staff from P is 45°. Find the length of the flag-staff and the distance of the building from the point P. (Take `sqrt3` = 1.732)
A tree standing on a horizontal plane is leaning towards the east. At two points situated at distances a and b exactly due west on it, the angles of elevation of the top are respectively α and β. Prove that the height of the top from the ground is `((b - a)tan alpha tan beta)/(tan alpha - tan beta)`
The angle of elevation of the top of a vertical tower PQ from a point X on the ground is 60°. At a point Y, 40 m vertically above X, the angle of elevation of the top is 45°. Calculate the height of the tower.
A vertical tower stands on a horizontal plane and is surmounted by a flagstaff of height 5 m. From a point on the ground the angles of elevation of the top and bottom of the flagstaff are 60° and 30° respectively. Find the height of the tower and the distance of the point from the tower. (take\[\sqrt{3}\]= 1.732)
In fig. 9 is shown a right circular cone of height 30 cm. A small cone is cut off from the top by a plane parallel to the base. If the volume of the small cone is 127127 of the volume of cone, find at what height above the base is the section made.
The angle of elevation of the top of a cell phone tower from the foot of a high apartment is 60° and the angle of depression of the foot of the tower from the top of the apartment is 30°. If the height of the apartment is 50 m, find the height of the cell phone tower. According to radiation control norms, the minimum height of a cell phone tower should be 120 m. State if the height of the above mentioned cell phone tower meets the radiation norms
As observed from the top of a 150 m high lighthouse from the sea level, the angles of depression of the two ships are 30° and 45°. If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships.
An electrician has to repair an electric fault on a pole of height 4 m. He needs to reach a point 1.3 m below the top of the pole to undertake the repair work. What should be the length of the ladder that he should use which when inclined at an angle of 60° to the horizontal would enable him to reach the required position?
An observer 1.5 metres tall is 20.5 metres away from a tower 22 metres high. Determine the angle of elevation of the top of the tower from the eye of the observer.
A person standing on the bank of a river observes that the angle of elevation of the top of a tree on the opposite bank of the river is 60° and when he retires 40 meters away from the tree the angle of elevation becomes 30°. The breadth of the river is ______.
