Question

A vertical tower stands on a horizontal plane and is surmounted by a flagstaff of height 5 m. From a point on the ground the angles of elevation of the top and bottom of the flagstaff are 60° and 30° respectively. Find the height of the tower and the distance of the point from the tower. (take\[\sqrt{3}\]= 1.732)

Answer 1

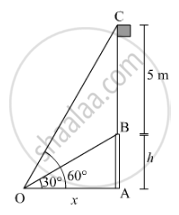
Let AB be the vertical tower and BC be the flagstaff.

Also, let O be the point on the ground from where the angles of elevation of the top and bottom of the flagstaff are 60° and 30°, respectively.

It is given that BC = 5 m.

Let the height of the vertical tower AB be h m and the distance of the point O from the tower be x m.

In ∆OAB,

\[\tan30^o = \frac{AB}{OA}\]
\[ \Rightarrow \frac{1}{\sqrt{3}} = \frac{h}{x}\]
\[ \Rightarrow x = \sqrt{3}h . . . . . \left( 1 \right)\]

In ∆OAC,

\[\tan60^o = \frac{AC}{OA}\]
\[ \Rightarrow \sqrt{3} = \frac{h + 5}{x}\]
\[ \Rightarrow x = \frac{h + 5}{\sqrt{3}} . . . . . \left( 2 \right)\]

From (1) and (2), we get

\[\sqrt{3}h = \frac{h + 5}{\sqrt{3}}\]
\[ \Rightarrow 3h = h + 5\]
\[ \Rightarrow 2h = 5\]
\[ \Rightarrow h = \frac{5}{2} = 2 . 5\]

Thus, the height of the tower is 2.5 m.

Substituting h = 2.5 in (1), we get

\[x = \sqrt{3} \times 2 . 5 = 1 . 732 \times 2 . 5 = 4 . 33\]

Therefore, the distance of the point O from the tower is 4.33 m.