Advertisements
Advertisements
प्रश्न
The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 45°. If the tower is 30 m high, find the height of the building.
उत्तर
Let AB be the building and CD be the tower.
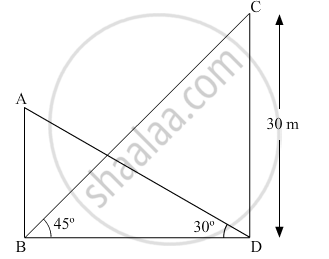
In ΔCDB,
`(CD)/(BD)=tan45^@`
`=>30/(BD)=1`
⇒BD=30 m
In ΔABD,
`(AB)/(BD)=tan30^@`
⇒AB=BD × `1/sqrt3`
`=>AB=30/sqrt3=10sqrt3m`
Therefore, the height of the building is `10sqrt3m`
APPEARS IN
संबंधित प्रश्न
From the top of a building 30 m high, the top and bottom of a tower are observed to have angles of depression 30º and 45º respectively. Find the height of the tower
A man observes a car from the top of a tower, which is moving towards the tower with a uniform speed. If the angle of depression of the car changes from 30° to 45° in 12 minutes, find the time taken by the car now to reach the tower.
The angle of elevation of an aeroplane from a point on the ground is 45°. After a flight of 15 seconds, the elevation changes to 30°. If the aeroplane is flying at a height of 3000 metres, find the speed of the aeroplane.
A solid right circular cone is cut into two parts at the middle of its height by a plane parallel to its base. The ratio of the volume of the smaller cone to the whole cone is
The tops of two poles of height 16 m and 10 m are connected by a wire of length lmetres. If the wire makes an angle of 30° with the horizontal, then l =
A road is flanked on either side by continuous rows of houses of height `4sqrt(3)` m with no space in between them. A pedestrian is standing on the median of the road facing a row house. The angle of elevation from the pedestrian to the top of the house is 30°. Find the width of the road
A portion of a 60 m long tree is broken by a tornado and the top struck up the ground making an angle of 30° with the ground level. The height of the point where the tree is broken is equal to ____________.
Find the angle of elevation of the sun when the shadow of a pole h metres high is `sqrt(3)` h metres long.
A vertical tower stands on a horizontal plane and is surmounted by a vertical flag staff of height h. At a point on the plane, the angles of elevation of the bottom and the top of the flag staff are α and β, respectively. Prove that the height of the tower is `((h tan α)/(tan β - tan α))`.
From the base of a pole of height 20 meter, the angle of elevation of the top of a tower is 60°. The pole subtends an angle 30° at the top of tower. Then the height of tower is ______.
