Advertisements
Advertisements
प्रश्न
A vertical tower stands on a horizontal plane and is surmounted by a vertical flag staff of height h. At a point on the plane, the angles of elevation of the bottom and the top of the flag staff are α and β, respectively. Prove that the height of the tower is `((h tan α)/(tan β - tan α))`.
उत्तर
Given that a vertical flag staff of height h is surmounted on a vertical tower of height H(say), such that FP = h and FO = H.
The angle of elevation of the bottom and top of the flag staff on the plane is ∠PRO = α and ∠FRO = β respectively.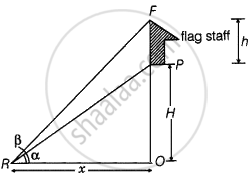
In ∆PRO, we have
tan α = `"PO"/"RO" = "H"/x` ...`[∵ tan θ = "Perpendicular"/"base"]`
⇒ x = `"H"/tan α` ...[Equation 1]
And in ∆FRO, we have
tan β = `"FO"/"RO" = ("FP" + "PO")/"RO"`
tan β = `("h" + "H")/x`
⇒ x = `("h" + "H")/tan β` ...[Equation 2]
Comparing equation 1 and equation 2,
⇒ `"H"/tan α = ("h" + "H")/tan β`
Solving for H,
⇒ H tan β = (h + H) tan α
⇒ H tan β – H tan α = h tan α
⇒ H (tan β – tan α) = h tan α
⇒ H = `("h" tan α)/(tan β - tan α)`
Hence, proved.
APPEARS IN
संबंधित प्रश्न
A vertical tower stands on a horizontal plane and is surmounted by a flagstaff of height 7m. At a point on the plane, the angle of elevation of the bottom of the flagstaff is 30º and that of the top of the flagstaff is 45º. Find the height of the tower.
As observed from the top of a 75 m high lighthouse from the sea-level, the angles of depression of two ships are 30° and 45°. If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships.
A boy is standing on the ground and flying a kite with 100 m of string at an elevation of 30°. Another boy is sanding on the roof of a 10 m high building and is flying his kite at an elevation of 45°. Both the boys are on opposite sides of both the kites. Find the length of the string that the second boy must have so that the two kites meet.
If the angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m from the base of the tower in the same straight line with it are complementary, find the height of the tower.
The ratio of the length of a rod and its shadow is `1 : sqrt3`. The angle of elevation of the sum is
On a morning walk, three persons step out together and their steps measure 30 cm, 36 cm, and 40 cm respectively. What is the minimum distance each should walk so that each can cover the same distance in complete steps?
A lift in a building of height 90 feet with transparent glass walls is descending from the top of the building. At the top of the building, the angle of depression to a fountain in the garden is 60°. Two minutes later, the angle of depression reduces to 30°. If the fountain is `30sqrt(3)` feet from the entrance of the lift, find the speed of the lift which is descending.
The angle of elevation of the top of a tower 30 m high from the foot of another tower in the same plane is 60°, then the distance between the two towers is ____________.
A person is standing at a distance of 50 m from a temple looking at its top. The angle of elevation is 45°. Find the height of the temple.
|
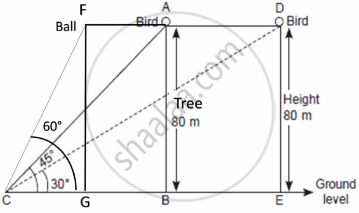
One evening, Kaushik was in a park. Children were playing cricket. Birds were singing on a nearby tree of height 80m. He observed a bird on the tree at an angle of elevation of 45°. When a sixer was hit, a ball flew through the tree frightening the bird to fly away. In 2 seconds, he observed the bird flying at the same height at an angle of elevation of 30° and the ball flying towards him at the same height at an angle of elevation of 60°.
|
- At what distance from the foot of the tree was he observing the bird sitting on the tree?
- How far did the bird fly in the mentioned time?
(or)
After hitting the tree, how far did the ball travel in the sky when Kaushik saw the ball? - What is the speed of the bird in m/min if it had flown `20(sqrt3 + 1) m`?