Advertisements
Advertisements
प्रश्न
A vertical tower stands on a horizontal plane and is surmounted by a flagstaff of height 7m. At a point on the plane, the angle of elevation of the bottom of the flagstaff is 30º and that of the top of the flagstaff is 45º. Find the height of the tower.
उत्तर १
Let AB be the tower and BC be the flagstaff.
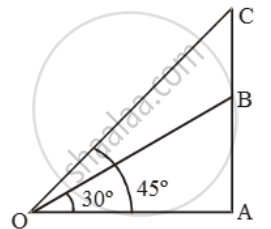
Then, BC = 7 m. Let AB = h.
Let O be the point of observation.
Then, ∠AOB = 30º and ∠AOC = 45º.
`\text{Now, }\frac{OA}{AC}=\text{cot 45}^\text{o}=1`
⇒ OA = AC = h + 7.
`\text{And, }\frac{OA}{AB}=\text{cot }30^\text{o}=\sqrt{3}`
`\Rightarrow \frac{OA}{h}=\sqrt{3}\Rightarrow OA=h\sqrt{3}`
∴ h + 7 = h√3
`\Rightarrow \frac{7}{\sqrt{3}-1}\times\frac{\sqrt{3}+1}{\sqrt{3}+1}=\frac{7(\sqrt{3}+1)}{2}=9.562\m`
उत्तर २
Let BC be the tower of height hm. AB be the flagstaff of height 7 m on the tower and Dbe the point on the plane making an angle of elevation of the top of the flagstaff is 45° and angle of elevation of the bottom of the flagstaff is 30°.
Let CD = x, AB = 7 and ∠BDC = 30° and ∠ADC = 45°.
We to find the height of the tower
We have the corresponding figure as follows
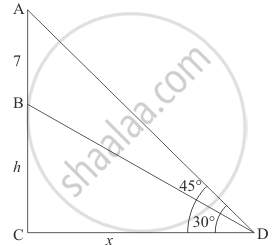
So we use trigonometric ratios.
In a triangle BCD
`=> tan D = (BC)/(CD)`
`=> tan 30^@ = h/x`
`=> 1/sqrt3 = h/x`
`=> x = sqrt3h`
Again in a triangle ADC
`=> tan D = (AB + BC)/(CD)`
`=> tan 45^@ = (h + 7)/x`
`=> 1 = (h + 7)/x`
`=> x = h + 7`
`=> sqrt3h = h + 7`
`=> h(sqrt3 - 1) = 7`
`=> h = 7/(sqrt3 - 1)`
`=> h = 9.56`
Hence the height of toweris 9.56 m
APPEARS IN
संबंधित प्रश्न
The angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m from the base of the tower and in the same straight line with it are 60° and 30° respectively. Find the height of the tower.
A tree breaks due to storm and the broken part bends so that the top of the tree touches the ground, making an angle 30° with it. The distance between the foot of the tree to the point where the top touches the ground is 8 m. Find the height of the tree.
The angle of elevation of a cloud from a point 60 m above the surface of the water of a lake is 30° and the angle of depression of its shadow in water of lake is 60°. Find the height of the cloud from the surface of water
The angle of elevation of the top of a tower from a point A on the ground is 30°. Moving a distance of 20metres towards the foot of the tower to a point B the angle of elevation increases to 60°. Find the height of the tower & the distance of the tower from the point A.
Two ships are approaching a light-house from opposite directions. The angles of depression of the two ships from the top of the light-house are 30° and 45°. If the distance between the two ships is 100 m, find the height of the light-house. \[[Use \sqrt{3} = 1 . 732]\]
What is the angle of elevation of the Sun when the length of the shadow of a vetical pole is equal to its height?
The tops of two poles of heights 20 m and 14 m are connected by a wire. If the wire makes an angle of 30° with the horizontal, then the length of the wire is ____________.
As observed from the top of a 150 m high lighthouse from the sea level, the angles of depression of the two ships are 30° and 45°. If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships.
Two vertical poles are 150 m apart and the height of one is three times that of the other. If from the middle point of the line joining their feet, an observer finds the angles of elevation of their tops to be complementary, then the height of the shorter pole (in meters) is ______.
The angle of elevation of the top of a 30 m high tower at a point 30 m away from the base of the tower is ______.
