Advertisements
Advertisements
प्रश्न
The angle of elevation of the top of a tower from a point A on the ground is 30°. Moving a distance of 20metres towards the foot of the tower to a point B the angle of elevation increases to 60°. Find the height of the tower & the distance of the tower from the point A.
उत्तर
Let h be the height of the tower and the angle of elevation of the top of the tower from a point A on the ground is 30° and on moving with distance 20 m towards the foot of tower on the point B is 60°.
Let AB = 20 and BC = x
Now we have to find the height of tower and distance of tower from point A.
So we use trigonometrical ratios.
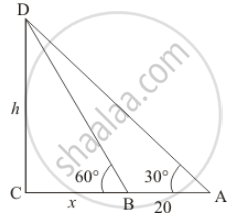
In ΔDBC
`=> tan D = (CD)/(BC)`
`=> tan 60^@ = (CD)/(BC)
`=> sqrt3 = h/x`
`=> x = h/sqrt3`
Again in Δ DAC
`=> tan A = (CD)/(BC + BA)`
`=> tan 30^@ = h/(x + 20)`
`=> 1/sqrt3 = h/(x + 20)`
`=> x = sqrt3h - 20`
`=> h/sqrt3 + 20 = sqrt3h`
`=> h/sqrt3 - sqrt3h = -20`
`=> h - 3h = -20sqrt3`
`=> -2h = -20sqrt3`
`=> h = 10sqrt3`
`=> h = 17.32`
`=> x = (10sqrt3)/sqrt3`
`=> x = 10`
So distance
`=> AC = x + 20`
=> AC = 30
Hence the required height is 17.32 m and distance is 30 m
APPEARS IN
संबंधित प्रश्न
The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 45°. If the tower is 30 m high, find the height of the building.
A balloon of radius γ makes an angle α at the eye of an observer and the angle of elevation of its centre is β. Then find the height of its centre from the ground level
An aeroplane when flying at a height of 4000m from the ground passes vertically above another aeroplane at an instant when the angles of the elevation of the two planes from the same point on the ground are 60º and 45º respectively. Find the vertical distance between the aeroplanes at that instant
A man on the deck of a ship is 10 m above the water level. He observes that the angle of elevation of the top of a cliff is 45° and the angle of depression of the base is 300. Calculate the distance of the cliff from the ship and the height of the cliff.
An aeroplane flying horizontally 1 km above the ground is observed at an elevation of 60°. After 10 seconds, its elevation is observed to be 30°. Find the speed of the aeroplane in km/hr.
The angle of elevation of a cloud from a point h metre above a lake is θ. The angle of depression of its reflection in the lake is 45°. The height of the cloud is
From the top of a lighthouse, the angle of depression of two ships on the opposite sides of it is observed to be 30° and 60°. If the height of the lighthouse is h meters and the line joining the ships passes through the foot of the lighthouse, show that the distance between the ships is `(4"h")/sqrt(3)` m
Three villagers A, B and C can see each other using telescope across a valley. The horizontal distance between A and B is 8 km and the horizontal distance between B and C is 12 km. The angle of depression of B from A is 20° and the angle of elevation of C from B is 30°. Calculate the vertical height between A and B. (tan 20° = 0.3640, `sqrt3` = 1.732)

An aeroplane is flying parallel to the Earth’s surface at a speed of 175 m/sec and at a height of 600 m. The angle of elevation of the aeroplane from a point on the Earth’s surface is 37°. After what period of time does the angle of elevation increase to 53°? (tan 53° = 1.3270, tan 37° = 0.7536)
In given figure, the length of AP is ____________.

