Advertisements
Advertisements
प्रश्न
From the top of a 15 m high building, the angle of elevation of the top of a tower is found to be 30°. From the bottom of the same building, the angle of elevation of the top of the tower is found to be 60°. Find the height of the tower and the distance between tower and the building.
उत्तर
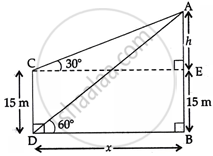
Let AB = tower
CD = building
Such that ∠ACE = 30°
∠ADB = 60°
AE = h m (say)
EB = CD = 15 m
and BD = x m (say)
= CE
Now, In ΔAEC, ∠E = 90° we have
`tan 30"°" = h/x`
⇒ `1/sqrt3 = h/x`
⇒ x = `sqrt3 * h` ...(i)
Again in ΔABD, ∠B = 90° we have
`tan 60"°" = (AB)/(BD)`
⇒ `sqrt3 = (h + 15)/x`
⇒ `sqrt3 * (sqrt3 * h) = h + 15` ...[∵ from (i) x = `sqrt3 .` h]
⇒ 3h − h = 15
⇒ h = 7.5 m
⇒ x = `sqrt3h = sqrt3 xx 7.5 ≈ 1.732 xx 7.5` m
x ≈ 12.99 m
Hence height of the tower = 7.5 + 15 = 22.5 m
and distance between tower and building = 12.99 m
संबंधित प्रश्न
A truck covers a distance of 150 km at a certain average speed and then covers another 200 km at an average speed which is 20 km per hour more than the first speed. If the truck covers the total distance in 5 hours, find the first speed of the truck.
A vertical tower stands on a horizontal plane and is surmounted by a flagstaff of height 7m. At a point on the plane, the angle of elevation of the bottom of the flagstaff is 30º and that of the top of the flagstaff is 45º. Find the height of the tower.
As observed from the top of a 75 m high lighthouse from the sea-level, the angles of depression of two ships are 30° and 45°. If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships.
A man observes a car from the top of a tower, which is moving towards the tower with a uniform speed. If the angle of depression of the car changes from 30° to 45° in 12 minutes, find the time taken by the car now to reach the tower.
The angle of elevation of a stationary cloud from a point 2500 m above a lake is 15° and the angle of depression of its reflection in the lake is 45°. What is the height of the cloud above the lake level? (Use tan 15° = 0.268)
The angle of elevation of the top Q of a vertical tower PQ from a point X on the ground is 60° . At a point Y, 40m vertically above X, the angle of elevation is 45° . Find the height of tower PQ.
The tops of two poles of height 16 m and 10 m are connected by a wire of length lmetres. If the wire makes an angle of 30° with the horizontal, then l =
A man is standing on the deck of a ship, which is 40 m above water level. He observes the angle of elevation of the top of a hill as 60° and the angle of depression of the base of the hill as 30°. Calculate the distance of the hill from the ship and the height of the hill `(sqrt(3) = 1.732)`
A plane is observed to be approaching the airport. It is at a distance of 12 km from the point of observation and makes an angle of elevation of 60°. The height above the ground of the plane is ____________.
The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 60 m high, find the height of the building.
