Advertisements
Advertisements
प्रश्न
The angle of elevation of a stationary cloud from a point 2500 m above a lake is 15° and the angle of depression of its reflection in the lake is 45°. What is the height of the cloud above the lake level? (Use tan 15° = 0.268)
उत्तर
Let AB be the surface of lake and P be the point of observation such that AP = 2500 m. Let C be the position of cloud and C' be the reflection in the lake. Then CB = C'B
Let PQ be the perpendicular from P on CB.
Let PQ = x m, CQ = h, QB = 2500 m. then CB = h + 2500 consequently C'B = h + 2500 m. and ∠CPQ - 15°, .∠QPC' = 45°

Here we have to find the height of cloud.
We use trigonometric ratios.
In ΔPCQ
`=> tan 15° = (CQ)/(PQ)`
`=> 2 - sqrt3 = h/x`
`=> x = h/(2 - sqrt3)`
Again in Δ PQC
`=> tan 45^@ = (QB + BC')/(PQ)`
`=> 1 = (2500 + h + 2500)//x`
`=> x = 5000 } h`
`=> h /()2 - sqrt3 = 5000 + h`
`=> h = 2500 (sqrt3 - 1)`
`=> CB = 2500 + 2500 (sqrt3 - 1)`
`=> CB = 2500sqrt3`
Hence the height of cloud is `2500sqrt3` m
APPEARS IN
संबंधित प्रश्न
From a point P on the ground the angle of elevation of a 10 m tall building is 30°. A flag is hoisted at the top of the building and the angle of elevation of the top of the flag-staff from P is 45°. Find the length of the flag-staff and the distance of the building from the point P. (Take `sqrt3` = 1.732)
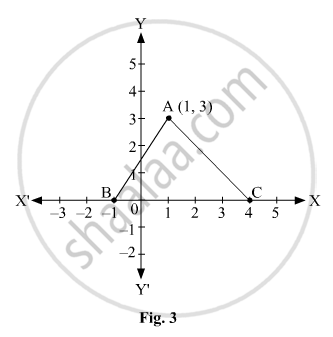
In Fig. 3, the area of triangle ABC (in sq. units) is:
It is found that on walking x meters towards a chimney in a horizontal line through its base, the elevation of its top changes from 30° to 60°. The height of the chimney is
The length of the shadow of a tower standing on level ground is found to be 2x metres longer when the sun's elevation is 30°than when it was 45°. The height of the tower in metres is
The height of the vertical pole is \[\sqrt{3}\] times the length of its shadow on the ground, then angle of elevation of the sun at that time is
If sin θ = cos θ , then 2 tan2θ + sin2θ – 1 is equal to
In given figure, AD = 4 cm, BD = 3 cm and CB = 12 cm. The value of tan `theta` is ____________.

A 1.5 m tall boy is standing at some distance from a 31.5 m tall building. If he walks ’d’ m towards the building the angle of elevation of the top of the building changes from 30° to 60°. Find the length d. (Take `sqrt3 = 1.73`)
If a man standing on a platform 3 metres above the surface of a lake observes a cloud and its reflection in the lake, then the angle of elevation of the cloud is equal to the angle of depression of its reflection.
A monkey is climbing a rope of length 15 m in a circus. The rope is tied to a vertical pole from its top. Find the height of the pole, if the angle, the rope makes with the ground level is equal to 60°.
