Advertisements
Advertisements
प्रश्न
If the angle of elevation of a cloud from a point h meters above a lake is a and the angle of depression of its reflection in the lake be b, prove that the distance of the cloud from the point of observation is `(2h sec alpha)/(tan beta - tan alpha)`
उत्तर
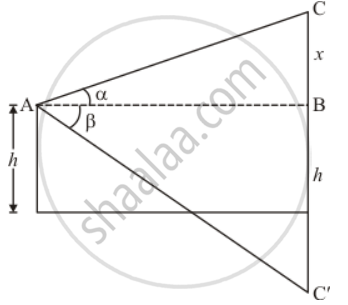
Let C′ be the image of cloud C. We have ∠CAB = α and ∠BAC' = β
Again let BC = x and AC be the distance of cloud from point of observation.
We have to prove that
`AC= (2h sec alpha)/(tan beta - tan alpha)`
The corresponding figure is as follows
We use trigonometric ratios.
in Δ ABC
`=> tan alpha = (BC)/(AB)`
`=> tan alpha = x/(AB)`
Again in Δ ABC'
`=> tan beta = (BC')/(AB)`
`=> tan beta = (x + 2h)/(AB)`
Now
`=> tan beta - tan alpha = (x + 2h)/(AB) - x/(AB)`
`=> tan bea - tan alpha = (2h)/(AB)`
`=> AB = (2h)/(tan beta - tan alpha)`
Again in Δ ABC
`=> cos alpha = (AB)/(AC)`
`=> AC = (AB)/(cos alpha)`
`=> (2h sec alpha)/(tan beta - tan alpha)`
Hence distance of cloud from points of observation is `(2h sec alpha)/(tan beta - tan alpha)`
APPEARS IN
संबंधित प्रश्न
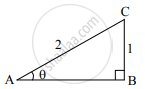
In the following figure, in ΔABC, BC = 1, AC = 2, ∠B = 90°. Find the value of sin θ.
The angles of depression of the top and bottom of 8 m tall building from the top of a multistoried building are 30° and 45° respectively. Find the height of the multistoried building and the distance between the two buildings.
From the top of a building AB, 60 m high, the angles of depression of the top and bottom of a vertical lamp post CD are observed to be 30° and 60° respectively. Find
1) the horizontal distance between AB and CD
2) the height of the lamp post.
3) the difference between the heights of the building and the lamp post.
A kite is flying at a height of 75 in from the level ground, attached to a string inclined at 60°. to the horizontal. Find the length of the string, assuming that there is no slack in it.
[Take `sqrt(3)` =1.732 ]
A statue 1.46m tall, stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the status is 60 and from the same point, the angle of elevation of the top of the pedestal is 45 . Find the height of the pedestal.
A storm broke a tree and the tree top rested on ground 20 m away from the
base of the tree, making an angle of 60o with the ground. Find the height
of the tree.
The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 60 m high, find the height of the building.
If the height of a tower and the distance of the point of observation from its foot, both, are increased by 10%, then the angle of elevation of its top ____________.
Find the angle of elevation of the sun when the shadow of a pole h metres high is `sqrt(3)` h metres long.
The angle of elevation of the top of a vertical tower from a point on the ground is 60°. From another point 10 m vertically above the first, its angle of elevation is 45°. Find the height of the tower.
