Advertisements
Advertisements
प्रश्न
If the angle of elevation of a cloud from a point h meters above a lake is a and the angle of depression of its reflection in the lake be b, prove that the distance of the cloud from the point of observation is `(2h sec alpha)/(tan beta - tan alpha)`
उत्तर
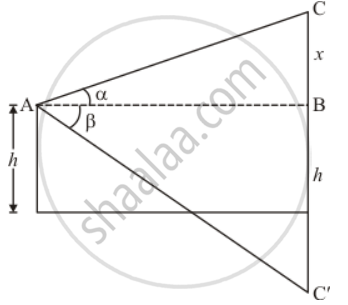
Let C′ be the image of cloud C. We have ∠CAB = α and ∠BAC' = β
Again let BC = x and AC be the distance of cloud from point of observation.
We have to prove that
`AC= (2h sec alpha)/(tan beta - tan alpha)`
The corresponding figure is as follows
We use trigonometric ratios.
in Δ ABC
`=> tan alpha = (BC)/(AB)`
`=> tan alpha = x/(AB)`
Again in Δ ABC'
`=> tan beta = (BC')/(AB)`
`=> tan beta = (x + 2h)/(AB)`
Now
`=> tan beta - tan alpha = (x + 2h)/(AB) - x/(AB)`
`=> tan bea - tan alpha = (2h)/(AB)`
`=> AB = (2h)/(tan beta - tan alpha)`
Again in Δ ABC
`=> cos alpha = (AB)/(AC)`
`=> AC = (AB)/(cos alpha)`
`=> (2h sec alpha)/(tan beta - tan alpha)`
Hence distance of cloud from points of observation is `(2h sec alpha)/(tan beta - tan alpha)`
APPEARS IN
संबंधित प्रश्न
From an aeroplane vertically above a straight horizontal road, the angles of depression of two consecutive milestones on opposite sides of the aeroplane are observed to be α and β. Show that the height in miles of the aeroplane above the road is given by `(tan alpha tan beta)/(tan alpha + tan beta)`
Two poles of equal heights are standing opposite to each other on either side of the road which is 80m wide, From a point P between them on the road, the angle of elevation of the top of one pole is 60 and the angle of depression from the top of another pole at P is 30 . Find the height of each pole and distance of the point P from the poles.
From the top of a lighthouse, an observer looking at a ship makes angle of depression of 60°. If the height of the lighthouse is 90 metre, then find how far the ship is from the lighthouse.
A boy standing at a distance of 48 meters from a building observes the top of the building and makes an angle of elevation of 30°. Find the height of the building.
If the angles of elevation of the top of a tower from two points distant a and b from the base and in the same straight line with it are complementary, then the height of the tower is
The angle of elevation of a cloud from a point h metres above a lake is β. The angle of depression of its reflection in the lake is 45°. The height of location of the cloud from the lake is
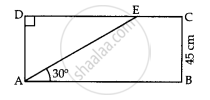
In given figure, the value of AE is ____________.
An observer `sqrt3` m tall is 3 m away from the pole `2 sqrt3` high. What is the angle of elevation of the top?
From the top of an 8 m high building, the angle of elevation of the top of a cable tower is 60° and the angle of depression of its foot is 45°. Determine the height of the tower. (Take `sqrt(3)` = 1.732).
Find the length of the shadow on the ground of a pole of height 18m when angle of elevation θ of the sun is such that tan θ = `6/7`.
