Advertisements
Advertisements
प्रश्न
A boy standing at a distance of 48 meters from a building observes the top of the building and makes an angle of elevation of 30°. Find the height of the building.
उत्तर
Let AB be the building and C be the position of the boy from the building.
Suppose the height of the building be h m.
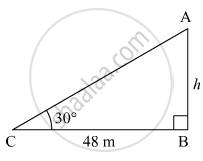
Here, BC = 48 m and ∠ACB = 30º.
In right ∆ABC,
\[\tan30^\circ = \frac{AB}{BC}\]
\[ \Rightarrow \frac{1}{\sqrt{3}} = \frac{h}{48}\]
\[ \Rightarrow h = \frac{48}{\sqrt{3}} = 16\sqrt{3} m\]
Thus, the height of the building is
\[16\sqrt{3}\]
संबंधित प्रश्न
The angles of elevation and depression of the top and the bottom of a tower from the top of a building, 60 m high, are 30° and 60° respectively. Find the difference between the heights of the building and the tower and the distance between them.
The banks of a river are parallel. A swimmer starts from a point on one of the banks and swims in a straight line inclined to the bank at 45º and reaches the opposite bank at a point 20 m from the point opposite to the starting point. Find the breadth of the river
The angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m. from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is 6 m.
Two points A and B are on the same side of a tower and in the same straight line with its base. The angles of depression of these points from the top of the tower are 60° and 45° respectively. If the height of the tower is 15 m, then find the distance between the points.
PQ is a post of given height a, and AB is a tower at some distance. If α and β are the angles of elevation of B, the top of the tower, at P and Q respectively. Find the height of the tower and its distance from the post.
A kite is flying at a height of 75 in from the level ground, attached to a string inclined at 60°. to the horizontal. Find the length of the string, assuming that there is no slack in it.
[Take `sqrt(3)` =1.732 ]
A military tent of height 8.25 m is in the form of a right circular cylinder of base diameter 30 m and height 5.5 m surmounted by a right circular cone of same base radius. Find the length of the canvas used in making the tent, if the breadth of the canvas is 1.5 m.
The height of a tower is 10 m. What is the length of its shadow when Sun's altitude is 45°?
If the angles of elevation of the top of a tower from two points distant a and b from the base and in the same straight line with it are complementary, then the height of the tower is
Two poles are 'a' metres apart and the height of one is double of the other. If from the middle point of the line joining their feet an observer finds the angular elevations of their tops to be complementary, then the height of the smaller is
On a morning walk, three persons step out together and their steps measure 30 cm, 36 cm, and 40 cm respectively. What is the minimum distance each should walk so that each can cover the same distance in complete steps?
The top of a 15 m high tower makes an angle of elevation of 60° with the bottom of an electronic pole and angle of elevation of 30° with the top of the pole. What is the height of the electric pole?
The angles of elevation and depression of the top and bottom of a lamp post from the top of a 66 m high apartment are 60° and 30° respectively. Find the height of the lamp post
The angles of elevation and depression of the top and bottom of a lamp post from the top of a 66 m high apartment are 60° and 30° respectively. Find the distance between the lamp post and the apartment `(sqrt(3) = 1.732)`
In figure given ABCD is a rectangle, the value of CE is ____________.

If the length of the shadow of a tower is increasing, then the angle of elevation of the sun ____________.
If a man standing on a platform 3 metres above the surface of a lake observes a cloud and its reflection in the lake, then the angle of elevation of the cloud is equal to the angle of depression of its reflection.
If one looks from a tower 10 m high at the top of a flag staff, the depression angle of 30° is made. Also, looking at the bottom of the staff from the tower, the angle of the depression made is of 60°. Find the height of the flag staff.
Two poles of heights 25 m and 35 m stand vertically on the ground. The tops of two poles are connected by a wire, which is inclined to the horizontal at an angle of 30°. Find the length of the wire and the distance between the poles.
