Advertisements
Advertisements
प्रश्न
The height of a tower is 10 m. What is the length of its shadow when Sun's altitude is 45°?
उत्तर
Let BC be the length of shadow is x m
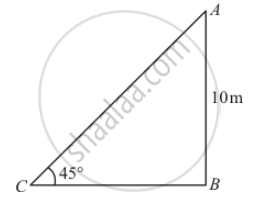
Given that: Height of tower is 10 meters and altitude of sun is 45°
Here we have to find length of shadow.
So we use trigonometric ratios.
In a triangle ABC,
`⇒ tan = (AB)/(BC)`
`⇒ tan 45°=(AB)/(AC)`
`⇒1=10/x`
`⇒x=10`
Hence the length of shadow is 10 m.
APPEARS IN
संबंधित प्रश्न
Two poles of equal heights are standing opposite each other an either side of the road, which is 80 m wide. From a point between them on the road, the angles of elevation of the top of the poles are 60° and 30º, respectively. Find the height of poles and the distance of the point from the poles.
The angle of elevation of the top of a tower from a point A on the ground is 30°. Moving a distance of 20metres towards the foot of the tower to a point B the angle of elevation increases to 60°. Find the height of the tower & the distance of the tower from the point A.
An aeroplane flying horizontally 1 km above the ground is observed at an elevation of 60°. After 10 seconds, its elevation is observed to be 30°. Find the speed of the aeroplane in km/hr.
The horizontal distance between two trees of different heights is 60 m. The angle of depression of the top of the first tree, when seen from the top of the second tree, is 45°. If the height of the second tree is 80 m, find the height of the first tree.
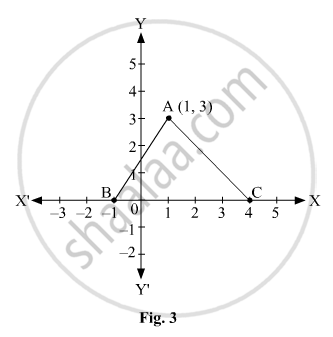
In Fig. 3, the area of triangle ABC (in sq. units) is:
A kite is flying at a height of 30 m from the ground. The length of string from the kite to the ground is 60 m. Assuming that there is no slack in the string, the angle of elevation of the kite at the ground is
The Distance of the point (−3, 4) from the x-axis is
From the top of a rock `50sqrt(3)` m high, the angle of depression of a car on the ground is observed to be 30°. Find the distance of the car from the rock
In given Fig., the angle of depression from the observing position D and E of the object at A are ____________.
Two vertical poles of different heights are standing 20m away from each other on the level ground. The angle of elevation of the top of the first pole from the foot of the second pole is 60° and angle of elevation of the top of the second pole from the foot of the first pole is 30°. Find the difference between the heights of two poles. (Take `sqrt(3)` = 1.73)
