Advertisements
Advertisements
प्रश्न
An aeroplane flying horizontally 1 km above the ground is observed at an elevation of 60°. After 10 seconds, its elevation is observed to be 30°. Find the speed of the aeroplane in km/hr.
उत्तर
An aeroplane is flying 1 km above the ground making an angle of elevation of aeroplane 60°. After 10 seconds angle of elevation is changed to 30°.
Let CE = x, BC = y, ∠AEB = 30°, ∠DEC = 60°, AB = 1 km and CD = 1 km.
Here we have to find the speed of an aeroplane.
The corresponding figure is as follows
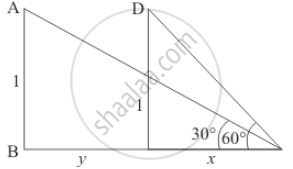
So we use trigonometric ratios.
In ΔDCE
`=> tan 60^@ = 1/x`
`=> sqrt3 = 1/x`
`=> x = 1/sqrt3`
Again in Δ ABE
`=> tan 30^@ = 1/(x + y)`
`=> 1/sqrt3 = 1/(x + y)`
`=> x + y = sqrt3`
`=> y = sqrt3 - 1/sqrt3`
`=> y = 2/sqrt3``
speed = "distance"/"time"`
`= y/(10 sec)`
`= (2/sqrt3)/(10/(60 xx 60))`
= 415.68
Hence the speed of aeroplace is 415.68 km/h.
APPEARS IN
संबंधित प्रश्न
The angle of depression of a car parked on the road from the top of a 150 m high tower is 30°. The distance of the car from the tower (in metres) is
`(A) 50sqrt3`
`(B) 150sqrt 3`
`(C) 150sqrt2`
`(D) 75`
A balloon is connected to a meteorological station by a cable of length 200 m, inclined at 60º to the horizontal. Find the height of the balloon from the ground. Assume that there is no slack in the cable
From a point on the ground 40 m away from the foot of a tower, the angle of elevation of the top of the tower is 30º. The angle of elevation of the top of a water tank (on the top of the tower) is 45º. Find the (i) height of the tower (ii) the depth of the tank.
From the top of a 7 m high building, the angle of elevation of the top of a cable tower is 60° and the angle of depression of its foot is 45°. Determine the height of the tower.
A straight highway leads to the foot of a tower. A man standing at the top of the tower observes a car as an angle of depression of 30°, which is approaching the foot of the tower with a uniform speed. Six seconds later, the angle of depression of the car is found to be 60°. Find the time taken by the car to reach the foot of the tower from this point.
As observed from the top of a 100 m high lighthouse from the sea-level, the angles of depression of two ships are 30° and 45°. If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships. [Use `sqrt3` = 1.732]
The angles of elevation of the top of a rock from the top and foot of a 100 m high tower are respectively 30° and 45°. Find the height of the rock.
An electrician has to repair an electric fault on a pole of height 4 meters. He needs to reach a point 1 meter below the top of the pole to undertake the repair work. What should be the length of the ladder that he should use, which when inclined at an angle of 60° to the horizontal would enable him to reach the required position?
If the angles of elevation of the top of a tower from two points distant a and b from the base and in the same straight line with it are complementary, then the height of the tower is
A man in a boat rowing away from a lighthouse 100 m high takes 2 minutes to change the angle of elevation of the top of the lighthouse from 60° to 30°.
Find the speed of the boat in metres per minute. [Use `sqrt(3` = 1.732]Use 3=1.732">
