Advertisements
Advertisements
प्रश्न
A straight highway leads to the foot of a tower. A man standing at the top of the tower observes a car as an angle of depression of 30°, which is approaching the foot of the tower with a uniform speed. Six seconds later, the angle of depression of the car is found to be 60°. Find the time taken by the car to reach the foot of the tower from this point.
उत्तर १
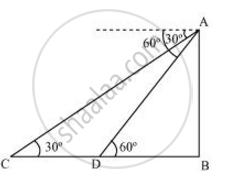
Let AB be the tower.
Initial position of the car is C, which changes to D after six seconds.
In ΔADB,
`("AB")/("DB") = tan 60º`
`("AB")/("DB") =sqrt3`
`"DB" = ("AB")/sqrt3`
In ΔABC,
`("AB")/("BC") = tan 30º`
`("AB")/("BD" + "DC") = 1/sqrt3`
`"AB"sqrt3 = "BD" + "DC"`
`"AB"sqrt3 = ("AB")/sqrt3 + "DC"`
`"DC" = "AB"sqrt3 - ("AB")/sqrt3 = "AB"(sqrt3 - 1/sqrt3)`
= `(2"AB")/sqrt3`
Time taken by the car to travel distance DC `("i.e" "2AB"/sqrt3)` = 6 second
Time taken by the car to travel distance DB `("i.e" ("AB")/sqrt3) = 6/((2"AB")/sqrt3)xx("AB")/sqrt3`
= `6/2`
= 3 seconds
उत्तर २
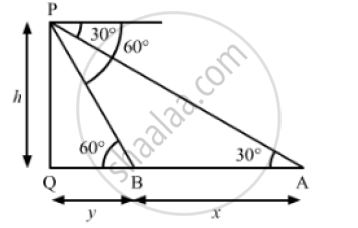
Let PQ be the tower.
We have,
∠PBQ = 60° and ∠PAQ = 30°
Let PQ = h, AB = x and BQ = y
In ΔAPQ,
`tan 30° = (PQ)/(AQ)`
⇒ `1/ sqrt(3) = h/(x+y) `
⇒ `x+y = h sqrt(3)` ...(1)
Also, in ΔBPQ,
`tan 60° = (PQ)/(BQ)`
⇒ `sqrt(3) = h/y`
⇒ `h = y sqrt(3) ` ...(2)
Substituting `h = y sqrt(3)` in (i), we get
`x +y = sqrt(3) (ysqrt(3))`
⇒ x + y = 3y
⇒ 3y - y = x
⇒ 2y = x
⇒ `y = x/2`
`"As, speed of the car from "A to B = (AB) /6 = x/6 "units"/ "sec"`
So, the time taken to reach the foot of the tower i.e. Q from B `(BQ)/(speed)`
= `y/((x/6))`
= `((x/2))/((x/6))`
= `6/2`
= 3 sec
So, the time taken to reach the foot of the tower from the given point is 3 seconds.
संबंधित प्रश्न
At a point A, 20 metres above the level of water in a lake, the angle of elevation of a cloud is 30˚. The angle of depression of the reflection of the cloud in the lake, at A is 60˚.
Find the distance of the cloud from A.
The angle of elevation of the top Q of a vertical tower PQ from a point X on the ground is 60°. From a point Y, 40 m vertically above X, the angle of elevation of the top Q of tower is 45. Find the height of the tower PQ and the distance PX. (Use `sqrt3=1.73)`
As observed from the top of a 75 m high lighthouse from the sea-level, the angles of depression of two ships are 30° and 45°. If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships.
Two points A and B are on the same side of a tower and in the same straight line with its base. The angles of depression of these points from the top of the tower are 60° and 45° respectively. If the height of the tower is 15 m, then find the distance between the points.
From a point on the ground 40m away from the foot of a tower, the angle of elevation of the top of the tower is 30 . The angle of elevation of the top of a water tank (on the top of the tower) is 45 , Find (i) the height of the tower, (ii) the depth of the tank.
The angle of elevation of the top of an unfinished tower at a distance of 75m from its base is 30° .How much higher must the tower be raised so that the angle of elevation of its top at the same point may be 60 .
The angle of elevation of the top Q of a vertical tower PQ from a point X on the ground is 60° . At a point Y, 40m vertically above X, the angle of elevation is 45° . Find the height of tower PQ.
A vertical tower stands on a horizontal plane and is surmounted by a flagstaff of height 5 m. From a point on the ground the angles of elevation of the top and bottom of the flagstaff are 60° and 30° respectively. Find the height of the tower and the distance of the point from the tower. (take\[\sqrt{3}\]= 1.732)
The angles of elevation and depression of the top and bottom of a light-house from the top of a 60 m high building are 30° and 60° respectively. Find (i) the difference between the heights of the light-house and the building. (ii) the distance between the light-house and the building.
From a point on the ground, 20 m away from the foot of a vertical tower, the angle elevation of the top of the tower is 60°, What is the height of the tower?
If the angles of elevation of a tower from two points distant a and b (a>b) from its foot and in the same straight line from it are 30° and 60°, then the height of the tower is
From a light house the angles of depression of two ships on opposite sides of the light house are observed to be 30° and 45°. If the height of the light house is h metres, the distance between the ships is
If the angle of elevation of a cloud from a point 200 m above a lake is 30° and the angle of depression of its reflection in the lake is 60°, then the height of the cloud above the lake is
The length of shadow of a tower on the plane ground is \[\sqrt{3}\] times the height of the tower. The angle of elevation of sun is
The height of the vertical pole is \[\sqrt{3}\] times the length of its shadow on the ground, then angle of elevation of the sun at that time is
The electric pole subtends an angle of 30° at a point on the same level as its foot. At a second point ‘b’ metres above the first, the depression of the foot of the pole is 60°. The height of the pole (in metres) is equal to
Two persons are standing ‘x’ metres apart from each other and the height of the first person is double that of the other. If from the middle point of the line joining their feet an observer finds the angular elevations of their tops to be complementary, then the height of the shorter person (in metres) is
An observer `sqrt3` m tall is 3 m away from the pole `2 sqrt3` high. What is the angle of elevation of the top?
The angle of elevation of the top of a tower 30 m high from the foot of another tower in the same plane is 60° and the angle of elevation of the top of the second tower from the foot of the first tower is 30°. Find the distance between the two towers and also the height of the other tower.
Two vertical poles of different heights are standing 20m away from each other on the level ground. The angle of elevation of the top of the first pole from the foot of the second pole is 60° and angle of elevation of the top of the second pole from the foot of the first pole is 30°. Find the difference between the heights of two poles. (Take `sqrt(3)` = 1.73)
