Advertisements
Advertisements
प्रश्न
The electric pole subtends an angle of 30° at a point on the same level as its foot. At a second point ‘b’ metres above the first, the depression of the foot of the pole is 60°. The height of the pole (in metres) is equal to
विकल्प
`sqrt(3)` b
`"b"/3`
`"b"/2`
`"b"/sqrt(3)`
उत्तर
`"b"/2`
Explanation;
Hint:
Let the height of the pole BC be h
AC = b + h
Let CD be x
In the right ∆BCD, tan 30° = `"BC"/"AB"`
`1/sqrt(3)= "h"/x`
x = `sqrt(3)`h ...(1)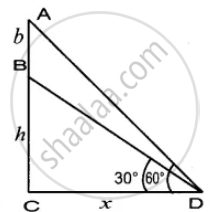
In the right ∆ACD, tan 60° = `"AC"/"CD"`
`sqrt(3) = ("b" + "h")/x`
x = `("b" + "h")/sqrt3` ....(2)
From (1) and (2) we get
`sqrt(3)`h = `("b" + "h")/sqrt(3)`
⇒ 3h = b + h
2h = b
⇒ h = `"b"/2`
APPEARS IN
संबंधित प्रश्न
At a point A, 20 metres above the level of water in a lake, the angle of elevation of a cloud is 30˚. The angle of depression of the reflection of the cloud in the lake, at A is 60˚.
Find the distance of the cloud from A.
A tower is 100√3 metres high. Find the angle of elevation of its top from a point 100 metres away from its foot.
A person observed the angle of elevation of the top of a tower as 30°. He walked 50 m towards the foot of the tower along level ground and found the angle of elevation of the top of the tower as 60°. Find the height of the tower.
A parachutist is descending vertically and makes angles of elevation of 45° and 60° at two observing points 100 m apart from each other on the left side of himself. Find the maximum height from which he falls and the distance of the point where he falls on the ground form the just observation point.
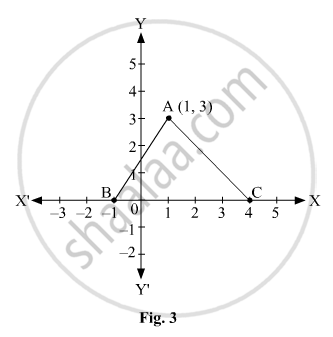
In Fig. 3, the area of triangle ABC (in sq. units) is:
A storm broke a tree and the treetop rested 20 m from the base of the tree, making an angle of 60° with the horizontal. Find the height of the tree.
If the angles of elevation of the top of a tower from two points distant a and b from the base and in the same straight line with it are complementary, then the height of the tower is
Two persons are a metres apart and the height of one is double that of the other. If from the middle point of the line joining their feet, an observer finds the angular elevation of their tops to be complementary, then the height of the shorter post is
The angles of depression of two objects from the top of a 100 m hill lying to its east are found to be 45° and 30°. Find the distance between the two objects. (Take `sqrt3 = 1.73`)
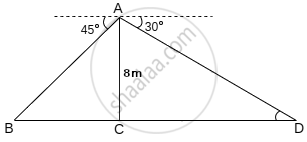
From a point on a bridge across a river, the angles of depression of the banks on opposite sides of the river are 30° and 45°. If the bridge is at a height of 8 m from the banks, then find the width of the river.