Advertisements
Advertisements
प्रश्न
From a point on a bridge across a river, the angles of depression of the banks on opposite sides of the river are 30° and 45°. If the bridge is at a height of 8 m from the banks, then find the width of the river.
उत्तर
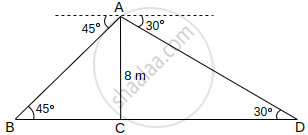
Clearly, ∠ABC = 45° and ∠ADC = 30° ....[∵ Angle of depression = Angle of elevation]
Now, In ΔABC, we have
tan 45° = `("AC")/("BC")`
⇒ 1 = `8/("BC")`
⇒ BC = 8 m ...(i)
Also, In ΔACD, we have
tan 30° = `("AC")/("DC")`
⇒ `1/sqrt(3) = 8/("DC")`
⇒ DC = `8sqrt(3)` ...(ii)
From equations (i) and (ii), we get
BD = BC + DC
= `8 + 8sqrt(3)`
= `8(sqrt(3) + 1)`
= 8(1.732 + 1)
= 8 × 2.732
= 21.856 m
APPEARS IN
संबंधित प्रश्न
The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 45°. If the tower is 30 m high, find the height of the building.
The angles of elevation and depression of the top and the bottom of a tower from the top of a building, 60 m high, are 30° and 60° respectively. Find the difference between the heights of the building and the tower and the distance between them.
A tree breaks due to storm and the broken part bends so that the top of the tree touches the ground, making an angle 30° with it. The distance between the foot of the tree to the point where the top touches the ground is 8 m. Find the height of the tree.
Two men on either side of the cliff 80 m high observe the angles of an elevation of the top of the cliff to be 30° and 60° respectively. Find the distance between the two men.
A fire in a building B is reported on the telephone to two fire stations P and Q, 20 km apart from each other on a straight road. P observes that the fire is at an angle of 60° to the road and Q observes that it is at an angle of 45° to the road. Which station should send its team and how much will this team have to travel?
From the top of a 50 m high tower, the angles of depression of the top and bottom of a pole are observed to be 45° and 60° respectively. Find the height of the pole.
A statue, 2 m tall, stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the statue is 60° and from the same point, the angle of elevation of the top of the pedestal is 45°. Find the height of the pedestal.
The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 60 m high, find the height of the building.
The angle of elevation of the top of a vertical tower from a point on the ground is 60°. From another point, 10 m vertically above the first, its angle of elevation is 45°. Find the height of the tower.
A monkey is climbing a rope of length 15 m in a circus. The rope is tied to a vertical pole from its top. Find the height of the pole, if the angle, the rope makes with the ground level is equal to 60°.
