Advertisements
Advertisements
प्रश्न
A tree breaks due to storm and the broken part bends so that the top of the tree touches the ground, making an angle 30° with it. The distance between the foot of the tree to the point where the top touches the ground is 8 m. Find the height of the tree.
उत्तर
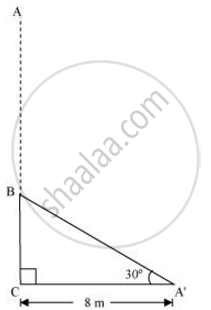
Let AC was the original tree. Due to storm, it was broken into two parts. The broken part A'B is making 30° with the ground.
In ΔABC
`("BC")/("AC") = tan 30º`
`("BC")/8 = 1/ sqrt3`
`"BC" = (8/sqrt3)m`
`("AC")/("AB") = cos 30º`
`8/("AB") = sqrt3/2`
`"AB" = ((16)/sqrt3)m`
Height of tree = AB + BC
= `(16/sqrt3+8/sqrt3)m`
= `24/sqrt3 m`
= `8sqrt3m`
Hence, the height of the tree is `8sqrt3 m`.
संबंधित प्रश्न
The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 45°. If the tower is 30 m high, find the height of the building.
The heights of two poles are 80 m and 62.5 m. If the line joining their tops makes an angle of 45º with the horizontal, then find the distance between the pole
An aeroplane when flying at a height of 4000m from the ground passes vertically above another aeroplane at an instant when the angles of the elevation of the two planes from the same point on the ground are 60º and 45º respectively. Find the vertical distance between the aeroplanes at that instant
An aeroplane is flying at a height of 300 m above the ground. Flying at this height, the angles of depression from the aeroplane of two points on both banks of a river in opposite directions are 45° and 60° respectively. Find the width of the river. [Use `sqrt3` = 1⋅732]
If the angle of elevation of a cloud from a point h meters above a lake is a and the angle of depression of its reflection in the lake be b, prove that the distance of the cloud from the point of observation is `(2h sec alpha)/(tan beta - tan alpha)`
The angles of elevation of the top of a tower from two points at distance of 5 metres and 20 metres from the base of the tower and is the same straight line with it, are complementary. Find the height of the tower.
A ladder 15 m long makes an angle of 60° with the wall. Find the height of the point where the ladder touches the wall.
A military tent of height 8.25 m is in the form of a right circular cylinder of base diameter 30 m and height 5.5 m surmounted by a right circular cone of same base radius. Find the length of the canvas used in making the tent, if the breadth of the canvas is 1.5 m.
If the angles of elevation of a tower from two points distant a and b (a>b) from its foot and in the same straight line from it are 30° and 60°, then the height of the tower is
From a light house the angles of depression of two ships on opposite sides of the light house are observed to be 30° and 45°. If the height of the light house is h metres, the distance between the ships is
The length of shadow of a tower on the plane ground is \[\sqrt{3}\] times the height of the tower. The angle of elevation of sun is
The angle of depression of a car, standing on the ground, from the top of a 75 m tower, is 30°. The distance of the car from the base of the tower (in metres) is
From the top of a lighthouse, an observer looks at a ship and finds the angle of depression to be 60° . If the height of the lighthouse is 84 meters, then find how far is that ship from the lighthouse? (√3 = 1.73)
A man in a boat rowing away from a lighthouse 100 m high takes 2 minutes to change the angle of elevation of the top of the lighthouse from 60° to 30°.
Find the speed of the boat in metres per minute. [Use `sqrt(3` = 1.732]Use 3=1.732">
A bird is flying from A towards B at an angle of 35°, a point 30 km away from A. At B it changes its course of flight and heads towards C on a bearing of 48° and distance 32 km away. How far is C to the East of B?
(sin 55° = 0.8192, cos 55° = 0.5736, sin 42° = 0.6691, cos 42° = 0.7431)
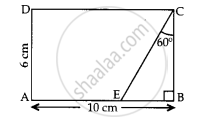
In given figure, the value of CE is ____________.
The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 60 m high, find the height of the building.
A boy 1.7 m tall is standing on a horizontal ground, 50 m away from a building. The angle of elevation of the top of the building from his eye is 60°. Calculate the height of the building. (Take `sqrt(3)` = 1.73)
A straight highway leads to the foot of a tower. A man standing on the top of the 75 m high tower observes two cars at angles of depression of 30° and 60°, which are approaching the foot of the tower. If one car is exactly behind the other on the same side of the tower, find the distance between the two cars. (use `sqrt(3)` = 1.73)
